【题目】列方程解应用题.
 程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).
程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).
在《算法统宗》里记载了一道趣题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完.试问大、小和尚各多少人?
参考答案:
【答案】大和尚有25人,小和尚有75人.
【解析】试题分析:设有x个小和尚,那么大和尚就有(100-x)个,小和尚吃馒头个数就是![]() x个,大和尚吃馒头个数就是 3×(100-x)个,根据大和尚吃馒头个数+小和尚吃馒头个数=100个可列方程即可求解.
x个,大和尚吃馒头个数就是 3×(100-x)个,根据大和尚吃馒头个数+小和尚吃馒头个数=100个可列方程即可求解.
试题解析:设小和尚有x人,则大和尚有(100 - x)人,
根据题意列方程,得![]() ,
,
解方程得:x = 75,
则100 – x = 100–75 = 25,
答:大和尚有25人,小和尚有75人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,I是△ABC三内角平分线的交点,IE⊥BC于E,AI延长线交BC于D,CI的延长线交AB于F,下列结论:①∠BIE=∠CID;②S△ABC=
 IE(AB+BC+AC);③BE=
IE(AB+BC+AC);③BE= (AB+BC﹣AC);④AC=AF+DC.其中正确的结论是_____.
(AB+BC﹣AC);④AC=AF+DC.其中正确的结论是_____.
-
科目: 来源: 题型:
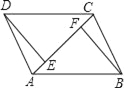
查看答案和解析>>【题目】已知,如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,DE=BF.
求证:(1)AF=CE;
(2)AB∥CD;
(3)AD=CB且AD∥CB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A.8的立方根是±2
B. 是一个最简二次根式
是一个最简二次根式
C.函数y=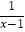 的自变量x的取值范围是x>1
的自变量x的取值范围是x>1
D.在平面直角坐标系中,点P(2,3)与点Q(﹣2,3)关于y轴对称 -
科目: 来源: 题型:
查看答案和解析>>【题目】小刚在课外书中看到这样一道有理数的混合运算题:
计算:

她发现,这个算式反映的是前后两部分的和,而这两部分之间存在着某种关系,利用这种关系,他顺利地解答了这道题。
(1)前后两部分之间存在着什么关系?
(2)先计算哪步分比较简便?并请计算比较简便的那部分。
(3)利用(1)中的关系,直接写出另一部分的结果。
(4)根据以上分析,求出原式的结果。
-
科目: 来源: 题型:
查看答案和解析>>【题目】水果市场将120吨水果运往各地商家,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型
甲
乙
丙
汽车运载量(吨/辆)
5
8
10
汽车运费(元/辆)
400
500
600
(1)若全部水果都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,市场可以调用甲、乙、丙三种车型参与运送(每种车型至少1辆),已知它们的总辆数为16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
-
科目: 来源: 题型:
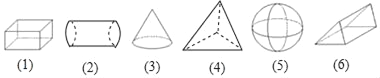
查看答案和解析>>【题目】下列请写出下列几何体,并将其分类.(只填写编号)
如果按“柱”“锥”“球”来分,柱体有_____,椎体有_____,球有_____;
如果按“有无曲面”来分,有曲面的有_____,无曲面的有_____.
相关试题

