【题目】如图所示,I是△ABC三内角平分线的交点,IE⊥BC于E,AI延长线交BC于D,CI的延长线交AB于F,下列结论:①∠BIE=∠CID;②S△ABC=![]() IE(AB+BC+AC);③BE=
IE(AB+BC+AC);③BE=![]() (AB+BC﹣AC);④AC=AF+DC.其中正确的结论是_____.
(AB+BC﹣AC);④AC=AF+DC.其中正确的结论是_____.

参考答案:
【答案】①②③.
【解析】①∵I为△ABC三条角平分线的交点,IE⊥BC于E,
∴∠ABI=∠IBD,
∵∠DIC=∠DAC+∠ACI=![]() (∠BAC+∠ACB),∠ABI=
(∠BAC+∠ACB),∠ABI=![]() ∠ABC,
∠ABC,
∴∠CID+∠ABI=90°,
∵IE⊥BC于E,
∴∠BIE+∠IBE=90°,
∵∠ABI=∠IBE,
∴∠BIE=∠CID;
即①成立;
②∵I是△ABC三内角平分线的交点,
∴点I到△ABC三边的距离相等,
∴S△ABC=S△ABI+S△BCI+S△ACI=![]() ABIE+
ABIE+![]() BCIE+
BCIE+![]() ACIE=
ACIE=![]() IE(AB+BC+AC),
IE(AB+BC+AC),
即②成立;
③如图,过I作IH⊥AB于H,IG⊥AC于G,

∵I是△ABC三内角平分线的交点,
∴IE=IH=IG,
在Rt△AHI与Rt△AGI中,
![]() ,
,
∴Rt△AHT≌Rt△AGI(HL),
∴AH=AG,同理BE=BH,CE=CG,
∴BE+BH=AB+BC﹣AH﹣CE=AB+BC﹣AC,
∴BE=![]() (AB+BC﹣AC);
(AB+BC﹣AC);
即③成立;
④由③证得IH=IE,
∵∠FHI=∠IED=90°,
∴△IHF与△DEI不一定全等,
∴HF不一定等于DE,
∴AC=AG+CG=AH+CE≠AF+CD,
即④错误.
故答案为:①②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数是( )

A. 400 B. 450 C. 500 D. 600
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践
背景阅读 早在三千多年前,我国周朝数学家商高就提出:将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”.它被记载于我国古代著名数学著作《周髀算经》中,为了方便,在本题中,我们把三边的比为3:4:5的三角形称为(3,4,5)型三角形,例如:三边长分别为9,12,15或3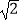 ,4
,4 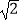 ,5
,5 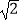 的三角形就是(3,4,5)型三角形,用矩形纸片按下面的操作方法可以折出这种类型的三角形.
的三角形就是(3,4,5)型三角形,用矩形纸片按下面的操作方法可以折出这种类型的三角形.
实践操作 如图1,在矩形纸片ABCD中,AD=8cm,AB=12cm.
第一步:如图2,将图1中的矩形纸片ABCD沿过点A的直线折叠,使点D落在AB上的点E处,折痕为AF,再沿EF折叠,然后把纸片展平.
第二步:如图3,将图2中的矩形纸片再次折叠,使点D与点F重合,折痕为GH,然后展平,隐去AF.
第三步:如图4,将图3中的矩形纸片沿AH折叠,得到△AD′H,再沿AD′折叠,折痕为AM,AM与折痕EF交于点N,然后展平.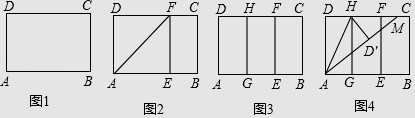
(1)请在图2中证明四边形AEFD是正方形.
(2)请在图4中判断NF与ND′的数量关系,并加以证明;
(3)请在图4中证明△AEN(3,4,5)型三角形;
(4)在不添加字母的情况下,图4中还有哪些三角形是(3,4,5)型三角形?请找出并直接写出它们的名称. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
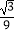 x2+
x2+ 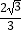 x+3
x+3 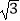 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).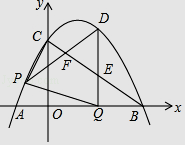
(1)求直线BC的函数表达式;
(2)①直接写出P,D两点的坐标(用含t的代数式表示,结果需化简)
②在点P、Q运动的过程中,当PQ=PD时,求t的值;
(3)试探究在点P,Q运动的过程中,是否存在某一时刻,使得点F为PD的中点?若存在,请直接写出此时t的值与点F的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
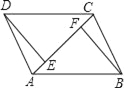
查看答案和解析>>【题目】已知,如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,DE=BF.
求证:(1)AF=CE;
(2)AB∥CD;
(3)AD=CB且AD∥CB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A.8的立方根是±2
B. 是一个最简二次根式
是一个最简二次根式
C.函数y=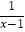 的自变量x的取值范围是x>1
的自变量x的取值范围是x>1
D.在平面直角坐标系中,点P(2,3)与点Q(﹣2,3)关于y轴对称 -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题.
 程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).
程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).在《算法统宗》里记载了一道趣题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完.试问大、小和尚各多少人?
相关试题

