【题目】水果市场将120吨水果运往各地商家,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部水果都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,市场可以调用甲、乙、丙三种车型参与运送(每种车型至少1辆),已知它们的总辆数为16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
参考答案:
【答案】(1) 分别需甲8辆、乙10辆;(2) 有二种运送方案:①甲车型6辆,乙车型5辆, 丙车型5辆;②甲车型4辆,乙车型10辆, 丙车型2辆
【解析】分析:(1)设需甲车型x辆,乙车型y辆,根据120吨水果和8200元运费列方程组求解;(2)设需甲车型x辆,乙车型y辆,丙车型z辆,根据水果120吨,16辆车列三元一次方程组,结合未知数的实际意义求解.
详解:(1)设需甲车型x辆,乙车型y辆,得:
![]() ,
,
解得![]() .
.
答:分别需甲车型8辆,乙车型10辆.
(2)设需甲车型x辆,乙车型y辆,丙车型z辆,得:
![]() ,
,
消去z得5x+2y=40,![]() ,
,
因x,y是正整数,且不大于16,得y=5或10,
由z是正整数,解得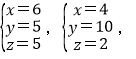
有二种运送方案:
①甲车型6辆,乙车型5辆,丙车型5辆;
②甲车型4辆,乙车型10辆,丙车型2辆
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学从A地出发,骑自行车在同一条路上行驶到距A地18千米的B地,他们离开A地的距离S(千米)和行驶时间t(小时)之间的函数关系图象如图所示,根据题目和图象所提供的信息,下列说法正确的是( )
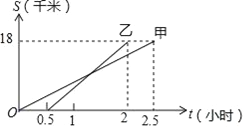
A. 乙比甲先到达B地
B. 乙在行驶过程中没有追上甲
C. 乙比甲早出发半小时
D. 甲的行驶速度比乙的行驶速度快
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上与表示-3的点相距5个单位长度的点所表示的数是_________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列具有相反意义的量的是( )
A.向西走20米与向南走30米B.胜2局与负三局
C.气温升高3℃与气温为-3℃D.盈利8万元与支出8万元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图的网格线是由边长为1的小正方形格子组成的, 小正方形的顶点叫格点,以格点为顶点的多边形叫格点多边形,小明研究发现,内部含有3个格点的四边形的面积与该四边形边上的格点数有某种关系,请你观察图中的4个格点四边形.设内部含有3个格点的四边形的面积为S,其各边上格点的个数之和为 m,则S与m的关系为( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个艺术窗的一部分,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形的边长为5cm,则正方形A、B、C、D的面积和是_____.

-
科目: 来源: 题型:
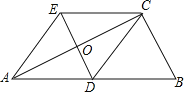
查看答案和解析>>【题目】在ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.
(1)求证:四边形ADCE是菱形;
(2)若AC=2DE,求sin∠CDB的值.
相关试题

