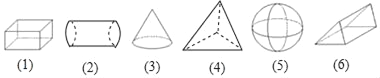
【题目】下列请写出下列几何体，并将其分类．（只填写编号）

如果按“柱”“锥”“球”来分，柱体有_____，椎体有_____，球有_____；

如果按“有无曲面”来分，有曲面的有_____，无曲面的有_____．

参考答案：

【答案】 （1）（2）（6） （3）（4） （5） （2）（3）（5） （1）（4）（6）

【解析】根据立体图形的特点从柱体的形状特征考虑．

按柱、锥、球分类．属于柱体有（1），（2），（6），椎体有（3），（4），球有（5）；

按“有无曲面”来分，有曲面的有（2），（3），（5），无曲面的有：（1），（4），（6）．

故答案为：（1），（2），（6）；（3），（4）；（5）；（2），（3），（5）；（1），（4），（6）．

关闭