【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列命题中正确的是( )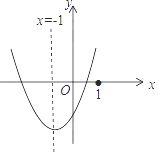
A.a>b>c
B.一次函数y=ax+c的图象不经第四象限
C.m(am+b)+b<a(m是任意实数)
D.3b+2c>0
参考答案:
【答案】D
【解析】解:A、由二次函数的图象开口向上可得a>0,由抛物线与y轴交于x轴下方可得c<0,由x=﹣1,得出﹣ ![]() =﹣1,故b>0,b=2a,则b>a>c,故此选项错误;
=﹣1,故b>0,b=2a,则b>a>c,故此选项错误;
B、∵a>0,c<0,∴一次函数y=ax+c的图象经一、三、四象限,故此选项错误;
C、当x=﹣1时,y最小,即a﹣b﹣c最小,故a﹣b+c<am2+bm+c,即m(am+b)+b>a,故此选项错误;
D.由图象可知x=1,a+b+c>0,
∵b=2a,
∴a= ![]() b,
b,
∴ ![]() b+b+c>0
b+b+c>0
∴3b+2c>0,故答案为:项正确;
故答案为:D.
利用二次函数的性质进行求解即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:
①abc<0;②3a+c>0;③4a+2b+c>0;④2a+b=0;⑤b2>4ac.
其中正确的结论的有( )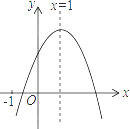
A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
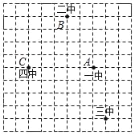
查看答案和解析>>【题目】某同学用10×10的方形网格绘制了遵义市四所初级中学(黑色格点)的位置图.(平方单位)
(1)请在适当的位置建立平面直角坐标系,并根据该平面直角坐标系解答下列问题;
(2)分别写出四所中学所在位置的坐标:一中 ,二中 ,三中 ,四中 ;
(3)分别记一中A、二中B、四中C,移动“三中”的位置于点D(请自行在图中标记),连接A、B、C、D四点组成的四边形ABCD为平行四边形.
①移动后所得D点的坐标是 (写一个点);
②求所得平行四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在
 和
和 中,
中,  ,
, ,
, .
.
(1)若
 三点在同一直线上,连接
三点在同一直线上,连接 交
交 于点
于点 ,求证:
,求证:  .
.(2)在第(1)问的条件下,求证:
 ;
;(3)将
 绕点
绕点 顺时针旋转得到图2,那么第(2)问中的结论是否依然成立?若成立,请证明你的结论:若不成立,请说明理由.
顺时针旋转得到图2,那么第(2)问中的结论是否依然成立?若成立,请证明你的结论:若不成立,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(
 ,y2)是抛物线上两点,则y1>y2 . 其中说法正确的是 .
,y2)是抛物线上两点,则y1>y2 . 其中说法正确的是 . 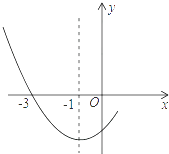
-
科目: 来源: 题型:
查看答案和解析>>【题目】科技发展,社会进步.中国己进入特色社会主义新时代,为实现“两个一百年”奋斗目标和中华民族伟大复兴的中国梦,需要人人奋斗.青少年时期是良好品格形成和知识积累的黄金时期.为此,大数据平台针对部分中学生品格表现和学习状况进行统计词查绘制如下统计图表,请根据图中提供的信息解决下列问题,类别:A.品格健全,成绩优异:B.尊敬师长,积极进取:C.自控力差,被动学习:D.沉迷奢玩,消极自卑
(1)本次调查被抽取的样本容量为 ;
(2)“自控力差,被动学习”的同学有 人,并补全条形统计图;
(3)样本中D类所在扇形的圆心角为 度;
(4)试根据你所在学校的总人数,估算D类学生人数,并谈谈你的想法.

-
科目: 来源: 题型:
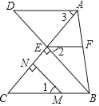
查看答案和解析>>【题目】如图,BE⊥AC与点E,MN⊥AC于点N,∠1=∠2,∠3=∠C,若∠AFE=80°,求∠DAF的度数.请根据解题过程“填空”或“说明理由”.
解:∵BE⊥AC,MN⊥AC
∴BE∥MN
∴∠1= ( )
又∵∠1=∠2
∴∠2= ( )
∴EF∥BC( )
∵∠3=∠C
∴AD∥BC
∴AD∥EF
∴∠DAF+∠AFE=180°( )
∴∠DAF=180°﹣∠AFE=180°﹣80°=100°.
相关试题

