搜索
【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图，有下列5个结论：
①abc＜0；②3a+c＞0；③4a+2b+c＞0；④2a+b=0；⑤b2＞4ac．
其中正确的结论的有（ ）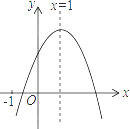
A.2个
B.3个
C.4个
D.5个
参考答案：
【答案】C
【解析】解：开口向下，则a＜0，
与y轴交于正半轴，则c＞0，
∵﹣ 
＞0，
∴b＞0，
则abc＜0，①正确；
∵﹣ =1，
则b=﹣2a，
∵a﹣b+c＜0，
∴3a+c＜0，②错误；
∵x=0时，y＞0，对称轴是x=1，
∴当x=2时，y＞0，
∴4a+2b+c＞0，③正确；
∵b=﹣2a，
∴2a+b=0，④正确；
∴b2﹣4ac＞0，
∴b2＞4ac，⑤正确．
故答案为：C．
根据二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定解答．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线
经过 
两点．
（1）求抛物线的解析式和顶点坐标；
（2）设点
为抛物线上一点，若 
，求点 的坐标． -
科目： 来源： 题型：
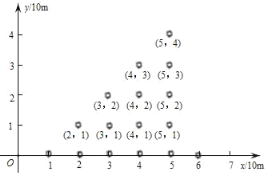
查看答案和解析>>【题目】某景区有一片树林，不仅树种相同，而且排列有序，如果用平面直角坐标系来表示每一棵的具体位置，从第一棵树开始依次表示为（1，0）→（2，0）→（2，1）→（3，2）→（3，1）→（3，0）→（4.0）→……，则第100棵树的位置是____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一次函数y=ax+b（a≠0）与二次函数y=ax2+2x+b（a≠0）在同一直角坐标系中的图象可能是（ ）
A.
B.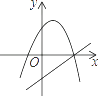
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某同学用10×10的方形网格绘制了遵义市四所初级中学（黑色格点）的位置图．（平方单位）
（1）请在适当的位置建立平面直角坐标系，并根据该平面直角坐标系解答下列问题；
（2）分别写出四所中学所在位置的坐标：一中 ，二中 ，三中 ，四中 ；
（3）分别记一中A、二中B、四中C，移动“三中”的位置于点D（请自行在图中标记），连接A、B、C、D四点组成的四边形ABCD为平行四边形．
①移动后所得D点的坐标是 （写一个点）；
②求所得平行四边形ABCD的面积．
-
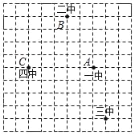
科目： 来源： 题型：
查看答案和解析>>【题目】如图1,在
和
中, 
,
,
.
(1)若
三点在同一直线上,连接
交
于点
,求证: 
.(2)在第(1)问的条件下,求证:
；(3)将
绕点
顺时针旋转得到图2,那么第(2)问中的结论是否依然成立?若成立,请证明你的结论:若不成立,请说明理由. -
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列命题中正确的是（ ）
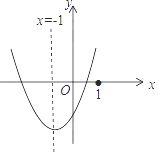
A.a＞b＞c
B.一次函数y=ax+c的图象不经第四象限
C.m（am+b）+b＜a（m是任意实数）
D.3b+2c＞0
相关试题
