【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)![]() 的顶点A、C的坐标分别为(-4,3)、(-1,1).
的顶点A、C的坐标分别为(-4,3)、(-1,1).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出![]() 关于y对称的△A′B′C′;
关于y对称的△A′B′C′;
(3)写出点![]() 的坐标 ;
的坐标 ;![]() 的面积为 .
的面积为 .
(4)若在y轴上有点M,则能使△ABM的周长最小的点M的坐标为 .

参考答案:
【答案】(1)见解析;(2)见解析;(3)(2,-1),4;(4)(0,![]() ).
).
【解析】
(1)根据A、C两点的坐标建立直角坐标系即可;
(2)分别作出各点关于y轴的对称点,再顺次连接即可;
(3)根据点B′在坐标系中的位置写出其坐标,利用割补法进行计算,即可得![]() 的面积;
的面积;
(4)利用待定系数法求出直线AB′的解析式,进而可得出在y轴上能使△ABM的周长最小的点M的坐标.
解:(1)坐标系如图;

(2)如图,△A′B′C′即为所求;
(3)由图可知,B′(2,-1),
S△ABC=3×4-![]() ×2×4-
×2×4-![]() ×2×3-
×2×3-![]() ×1×2
×1×2
=12-4-3-1
=4;
(4)如图所示,点M即为所求点,
设直线AB′的解析式为y=kx+b(k≠0),
∵(-4,3),B′(2,-1),
∴![]() ,解得
,解得 ,
,
∴直线AB′的解析式为![]() .
.
∵当x=0时,y=![]() ,
,
∴M(0,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某港口有一灯塔
 ,灯塔
,灯塔 的正东有
的正东有 、
、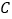 两灯塔,以
两灯塔,以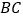 为直径的半圆区域内有若干暗礁,
为直径的半圆区域内有若干暗礁,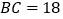 海里,一船在
海里,一船在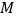 处测得灯塔
处测得灯塔 、
、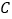 分别在船的
分别在船的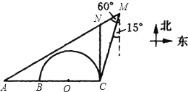
南偏西
 和南偏西
和南偏西 方向,船沿
方向,船沿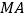 方向行驶
方向行驶 海里恰好处在灯塔
海里恰好处在灯塔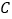 的正北方向
的正北方向 处.
处.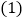 求
求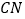 的长(精确到
的长(精确到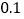 海里);
海里);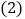 若船继续沿
若船继续沿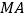 方向朝
方向朝 行驶,是否有触礁的危险?
行驶,是否有触礁的危险?(参考数值:
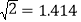 ,
,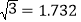 ,
,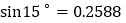 ,
,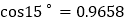 ,
,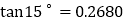 ,
, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知A、B、C、D四点的坐标依次为(0,0)、(6,0)(8,6)、(2,6),若一次函数y=mx﹣6m的图象将四边形ABCD的面积分成1:3两部分,则m的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,垂足为D,AD=4,BD=2,CD=8.

(1)求证:∠BAC=90°;
(2)P为BC边上一点,连接AP,若△ABP为等腰三角形,请求出BP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市准备在相距
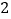 千米的
千米的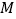 ,
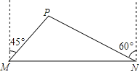
, 两工厂间修一条笔直的公路,但在
两工厂间修一条笔直的公路,但在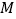 地北偏东
地北偏东 方向、
方向、 地北偏西
地北偏西 方向的
方向的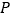 处,有一个半径为
处,有一个半径为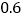 千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据:
千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据: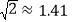 ,
,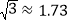 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,埃航
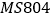 客机失事后,国家主席亲自发电进行慰问,埃及政府出动了多艘舰船和飞机进行搜救,其中一艘潜艇在海面下
客机失事后,国家主席亲自发电进行慰问,埃及政府出动了多艘舰船和飞机进行搜救,其中一艘潜艇在海面下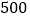 米的
米的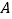 点处测得俯角为
点处测得俯角为 的前下方海底有黑匣子信号发出,继续沿原方向直线航行
的前下方海底有黑匣子信号发出,继续沿原方向直线航行 米后到达
米后到达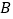 点,在
点,在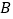 处测得俯角为
处测得俯角为 的前下方海底有黑匣子信号发出,求海底黑匣子
的前下方海底有黑匣子信号发出,求海底黑匣子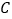 点距离海面的深度(结果保留根号).
点距离海面的深度(结果保留根号).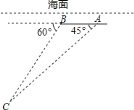
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速
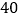 千米/时,已知交警测速点
千米/时,已知交警测速点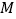 到该公路
到该公路 点的距离为
点的距离为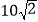 米,
米,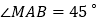 ,
,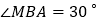 (如图所示),现有一辆汽车由
(如图所示),现有一辆汽车由 往
往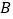 方向匀速行驶,测得此车从
方向匀速行驶,测得此车从 点行驶到
点行驶到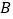 点所用的时间为
点所用的时间为 秒.
秒.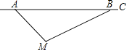
 求测速点
求测速点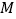 到该公路的距离;
到该公路的距离;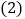 通过计算判断此车是否超速.(参考数据:
通过计算判断此车是否超速.(参考数据: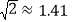 ,
,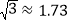 ,
,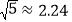 )
)
相关试题

