搜索
【题目】如图，某港口有一灯塔
，灯塔的正东有
、
两灯塔，以
为直径的半圆区域内有若干暗礁，
海里，一船在
处测得灯塔、分别在船的
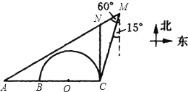
南偏西
和南偏西
方向，船沿
方向行驶
海里恰好处在灯塔的正北方向
处．
求
的长（精确到
海里）；
若船继续沿方向朝行驶，是否有触礁的危险？
（参考数值：
，
，
，
，
，
）
参考答案：
【答案】（1）1.64（2）没有触礁的危险
【解析】
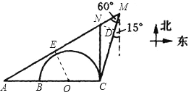
（1）设BC的中点是O，作ND⊥CM，OE⊥AM．在直角△NDM中利用∠NMC的三角函数求出ND的长，在直角△NCD中利用三角函数求出CN的长即可．（2）计算出OE的长，然后比较与9海里的大小关系就可以确定是否有危险．
设
的中点为
，作
，
，垂足分别为
、
．
在直角
中，
（海里），
在直角
中，
海里．
在直角
中，
海里，
∴
（海里），
∴
（海里），
∵
，
所以船继续沿
方向朝
行驶，没有触礁的危险．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，O为菱形ABCD对角线的交点，M是射线CA上的一个动点（点M与点C、O、A都不重合），过点A、C分别向直线BM作垂线段，垂足分别为E、F，连接OE，OF．
（1）①依据题意补全图形；
②猜想OE与OF的数量关系为_________________.
（2）小东通过观察、实验发现点M在射线CA上运动时，（1）中的猜想始终成立．
小东把这个发现与同学们进行交流，通过讨论，形成了证明（1）中猜想的几种想法：
想法1：由已知条件和菱形对角线互相平分，可以构造与△OAE全等的三角形，从而得到相等的线段，再依据直角三角形斜边中线的性质，即可证明猜想；
想法2：由已知条件和菱形对角线互相垂直，能找到两组共斜边的直角三角形，例如其中的一组△OAB和△EAB，再依据直角三角形斜边中线的性质，菱形四边相等，可以构造一对以OE和OF为对应边的全等三角形，即可证明猜想．
……
请你参考上面的想法，帮助小东证明（1）中的猜想（一种方法即可）．
（3）当∠ADC=120°时，请直接写出线段CF，AE，EF之间的数量关系是_________________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为美化小区环境，某小区有一块面积为30m2的等腰三角形草地，测得其一边长为10m，现要给这块三角形草地围上白色的低矮栅栏，则其长度为 m．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点E在△DBC的边DB上，点A在△DBC内部，∠DAE=∠BAC=90°，AD=AE，AB=AC．给出下列结论：
①BD=CE；②∠ABD+∠ECB=45°；③BD⊥CE；④BE2=2（AD2+AB2）﹣CD2．其中正确的是（ ）
A. ①②③④ B. ②④ C. ①②③ D. ①③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，已知A、B、C、D四点的坐标依次为（0，0）、（6，0）（8，6）、（2，6），若一次函数y=mx﹣6m的图象将四边形ABCD的面积分成1：3两部分，则m的值为_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AD⊥BC，垂足为D，AD＝4，BD＝2，CD＝8．
（1）求证：∠BAC＝90°；
（2）P为BC边上一点，连接AP，若△ABP为等腰三角形，请求出BP的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）
的顶点A、C的坐标分别为（-4，3）、（-1，1）．（1）请在如图所示的网格平面内作出平面直角坐标系；
（2）请作出
关于y对称的△A′B′C′；（3）写出点
的坐标 ；的面积为 ．（4）若在y轴上有点M，则能使△ABM的周长最小的点M的坐标为 .
相关试题
