【题目】已知:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q在⊙O上,连接PQ.
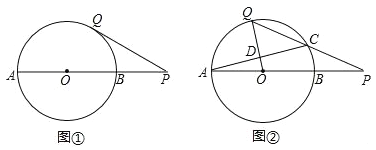
(1)如图①,线段PQ所在的直线与⊙O相切,求线段PQ的长;
(2)如图②,线段PQ与⊙O还有一个公共点C,且PC=CQ,连接OQ,AC交于点D.
①判断OQ与AC的位置关系,并说明理由;
②求线段PQ的长.
参考答案:
【答案】(1)![]() ;(2)①OQ⊥AC,理由见试题解析;②
;(2)①OQ⊥AC,理由见试题解析;②![]() .
.
【解析】试题分析:(1)如图①,连接OQ.利用切线的性质和勾股定理来求PQ的长度;
(2)如图②,连接BC.由三角形中位线得到BC∥OQ.利用圆周角定理得到BC⊥AC,故OQ⊥AC;
(3)利用割线定理来求PQ的长度.
试题解析:(1)如图①,连接OQ.∵线段PQ所在的直线与⊙O相切,点Q在⊙O上,∴OQ⊥OP.又∵BP=OB=OQ=2,∴PQ=![]() =
=![]() =
=![]() ,即PQ=
,即PQ=![]() ;
;
(2)OQ⊥AC.理由如下:如图②,连接BC.∵BP=OB,∴点B是OP的中点,又∵PC=CQ,∴点C是PQ的中点,∴BC是△PQO的中位线,∴BC∥OQ.又∵AB是直径,∴∠ACB=90°,即BC⊥AC,∴OQ⊥AC;
(3)如图②,PCPQ=PBPA,即![]() =2×6,解得PQ=
=2×6,解得PQ=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程x2+5x+a=0有一个根为﹣2,则a的值是( )
A. 6B. ﹣6C. 14D. ﹣14
-
科目: 来源: 题型:
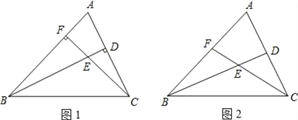
查看答案和解析>>【题目】已知△ABC,点D、F分别为线段AC、AB上两点,连接BD、CF交于点E.
(1)若BD⊥AC,CF⊥AB,如图1所示,试说明∠BAC+∠BEC=180°;
(2)若BD平分∠ABC,CF平分∠ACB,如图2所示,试说明此时∠BAC与∠BEC的数量关系;
(3)在(2)的条件下,若∠BAC=60°,试说明:EF=ED.
-
科目: 来源: 题型:
查看答案和解析>>【题目】①
 ② 124×122﹣1232
② 124×122﹣1232 ③-2x(x-5)-(x+2)(x-3) ④(z+x+y)(﹣z+x+y)
-
科目: 来源: 题型:
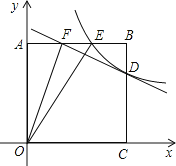
查看答案和解析>>【题目】如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4).
(1)求反比例函数的解析式;
(2)反比例函数的图象与线段BC交于点D,直线
 过点D,与线段AB相交于点F,求点F的坐标;
过点D,与线段AB相交于点F,求点F的坐标;(3)连接OF,OE,探究∠AOF与∠EOC的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在“6·26国际禁毒日”前组织七年级全体学生320人进行了一次“毒品预防知识”竞赛,赛后随机抽取了部分学生成绩进行统计,制作了频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题:
分数段(
 表示分数)
表示分数)频数
频率
50≤
 <60
<604
0.1
60≤
 <70
<70
0.2
70≤
 <80
<8012

80≤
 <90
<9010
0.25
90≤
 <100
<1006
0.15

(1)表中
 = ,
= ,  = ,并补全直方图;
= ,并补全直方图;(2)若用扇形统计图描述此成绩统计分布情况,则分数段80≤
 <100对应扇形的圆心角度数是 ;
<100对应扇形的圆心角度数是 ;(3)请估计该年级分数在60≤
 <70的学生有多少人?
<70的学生有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】(a+2)2+4|b-5|=0,求(7a+8b)-(-4a+6b)的值.
相关试题

