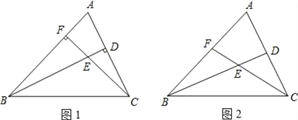
【题目】已知△ABC,点D、F分别为线段AC、AB上两点,连接BD、CF交于点E.
(1)若BD⊥AC,CF⊥AB,如图1所示,试说明∠BAC+∠BEC=180°;
(2)若BD平分∠ABC,CF平分∠ACB,如图2所示,试说明此时∠BAC与∠BEC的数量关系;
(3)在(2)的条件下,若∠BAC=60°,试说明:EF=ED.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】分析:(1)根据余角的性质得到∠DEC=∠BAC,由于∠DEC+∠BEC=180°,即可得到结论;(2)根据角平分线的性质得到∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠ACB,于是得到结论;(3)作∠BEC的平分线EM交BC于M,由∠BAC=60°,得到∠BEC=90°+
∠ACB,于是得到结论;(3)作∠BEC的平分线EM交BC于M,由∠BAC=60°,得到∠BEC=90°+![]() ∠BAC=120°,求得∠FEB=∠DEC=60°,根据角平分线的性质得到∠BEM=60°,推出△FBE≌△EBM,根据全等三角形的性质得到EF=EM,同理DE=EM,即可得到结论.
∠BAC=120°,求得∠FEB=∠DEC=60°,根据角平分线的性质得到∠BEM=60°,推出△FBE≌△EBM,根据全等三角形的性质得到EF=EM,同理DE=EM,即可得到结论.
本题解析:
(1)∵BD⊥AC,CF⊥AB,
∴∠DCE+∠DEC=∠DCE+∠FAC=90°,
∴∠DEC=∠BAC,∠DEC+∠BEC=180°,
∴∠BAC+∠BEC=180°;
(2)∵BD平分∠ABC,CF平分∠ACB,
∴∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠ACB,∠BEC=180°(∠EBC+∠ECB)=180°
∠ACB,∠BEC=180°(∠EBC+∠ECB)=180°![]() (∠ABC+∠ACB)=180
(∠ABC+∠ACB)=180![]() (180°∠BAC)=90°+
(180°∠BAC)=90°+![]() ∠BAC,
∠BAC,
(3)作∠BEC的平分线EM交BC于M,
∵∠BAC=60°,
∴∠BEC=90°+![]() ∠BAC=120°,
∠BAC=120°,
∴∠FEB=∠DEC=60°,
∵EM平分∠BEC,
∴∠BEM=60°,
在△FBE与△EBM中,
∠FBE=∠EBMBE=BE∠FEB=∠MEB,
∴△FBE≌△EBM,
∴EF=EM,同理DE=EM,
∴EF=DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
A. 5 B. ﹣5 C. 5或1 D. 以上都不对
-
科目: 来源: 题型:
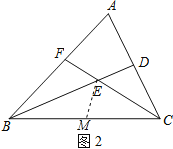
查看答案和解析>>【题目】某学校为了解该校学生的课余活动情况,抽样调查了部分同学,将所得数据处理后,制成折线统计图(部分)和扇形统计图(部分)如下:
(1)在这次研究中,一共调查了 名学生.
(2)补全频数分布折线图;
(3)该校共有2200名学生,估计该校学生中爱好阅读的人数大约是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程x2+5x+a=0有一个根为﹣2,则a的值是( )
A. 6B. ﹣6C. 14D. ﹣14
-
科目: 来源: 题型:
查看答案和解析>>【题目】①
 ② 124×122﹣1232
② 124×122﹣1232 ③-2x(x-5)-(x+2)(x-3) ④(z+x+y)(﹣z+x+y)
-
科目: 来源: 题型:
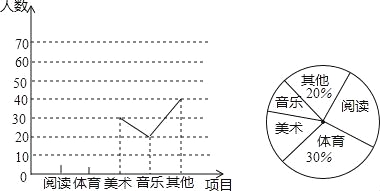
查看答案和解析>>【题目】已知:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q在⊙O上,连接PQ.
(1)如图①,线段PQ所在的直线与⊙O相切,求线段PQ的长;
(2)如图②,线段PQ与⊙O还有一个公共点C,且PC=CQ,连接OQ,AC交于点D.
①判断OQ与AC的位置关系,并说明理由;
②求线段PQ的长.
-
科目: 来源: 题型:
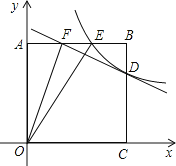
查看答案和解析>>【题目】如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4).
(1)求反比例函数的解析式;
(2)反比例函数的图象与线段BC交于点D,直线
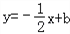 过点D,与线段AB相交于点F,求点F的坐标;
过点D,与线段AB相交于点F,求点F的坐标;(3)连接OF,OE,探究∠AOF与∠EOC的数量关系,并证明.
相关试题

