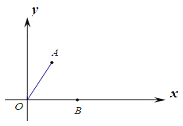
【题目】如图,在平面直角坐标系中,A(1,![]() ),B(2,0),C点在x轴上运动,过点O作直线AC的垂线,垂足为D.当点C在x轴上运动时,点D也随之运动.则线段BD长的最大值为______________.
),B(2,0),C点在x轴上运动,过点O作直线AC的垂线,垂足为D.当点C在x轴上运动时,点D也随之运动.则线段BD长的最大值为______________.
参考答案:
【答案】![]() +1
+1
【解析】根据圆周角定理的推论可得出点D在以AO中点E为圆心,AO为直径的圆上,连接BE并延长交圆E于点D,此时BD最长,利用等边三角形的性质即可求出BD的最大值.
∵OE垂直于直线AC,垂足为D,
作AO的中点E,
∴点D在以E为圆心,AO长为直径的圆上(如图1所示),
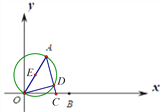
图1
连接BE并延长交圆E于点D,此时BD最长(如图2所示),
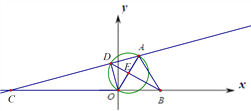
图2
连接AB,,
∵A(1,![]() ),
),
∴![]() 且
且![]() ,
,
∴![]() ,
,
∵B(2,0),
∴OB=2,
∴![]() 为等边三角形,
为等边三角形,
∵E是AO的中点,
∴ED=OE=![]() AO=1,
AO=1,
∴BE=![]()
∴BD=BE+ED=![]() +1.
+1.
故答案为:![]() +1.
+1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若点A在数轴上对应的数为
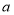 ,点B在数轴上对应的数为b,且
,点B在数轴上对应的数为b,且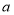 ,b满足
,b满足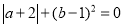
(1)求线段AB的长;
(2)点C在数轴上对应的数为x,且x是方程
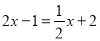 的解,在数轴上是否存在点P,使得PA+PB=PC?若存在,求出点P对应的数;若不存在,说明理由;
的解,在数轴上是否存在点P,使得PA+PB=PC?若存在,求出点P对应的数;若不存在,说明理由;(3)在(1)(2)条件下,点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒4个单位长度和9个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,请问:AB﹣BC的值是否随时间t的变化而改变?若变化,请说明理由;若不变,请求其常数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
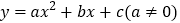 的对称轴为直线
的对称轴为直线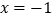 ,且抛物线与
,且抛物线与 轴交于
轴交于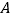 、
、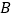 两点,与
两点,与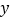 轴交于
轴交于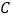 点,其中
点,其中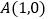 ,
,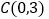 .
.
(1)若直线
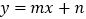 经过
经过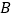 、
、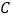 两点,求直线
两点,求直线 和抛物线的解析式;
和抛物线的解析式;(2)在抛物线的对称轴
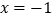 上找一点
上找一点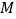 ,使点
,使点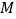 到点
到点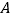 的距离与到点
的距离与到点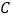 的距离之和最小,求出点
的距离之和最小,求出点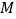 的坐标;
的坐标;(3)设点
 为抛物线的对称轴
为抛物线的对称轴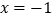 上的一个动点,求使
上的一个动点,求使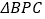 为直角三角形的点
为直角三角形的点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C在⊙O上,AD垂直于过点C的切线,垂足为D,且∠BAD=80°,则∠DAC的度数是_____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业500名员工参加安全生产知识测试,成绩记为A,B,C,D,E共5个等级,为了解本次测试的成绩(等级)情况,现从中随机抽取部分员工的成绩(等级),统计整理并制作了如下的统计图:
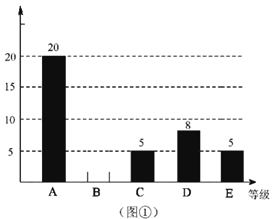
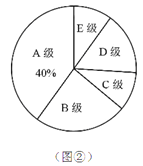
(1)求这次抽样调查的样本容量,并补全图①;
(2)如果测试成绩(等级)为A,B,C级的定为优秀,请估计该企业参加本次安全生产知识测试成绩(等级)达到优秀的员工的总人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法错误的是( ).
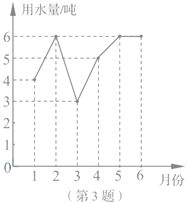
A、众数是6吨 B、平均数是5吨 C、中位数是5吨 D、方差是
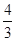
-
科目: 来源: 题型:
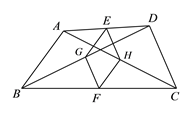
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=DC,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点.
(1)求证:四边形EGFH是菱形;
(2)若AB=4,且BA、CD延长后相交所成的锐角是60°,求四边形EGFH的面积.
相关试题

