【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且抛物线与
,且抛物线与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() ,
,![]() .
.

(1)若直线![]() 经过
经过![]() 、
、![]() 两点,求直线
两点,求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,求出点
的距离之和最小,求出点![]() 的坐标;
的坐标;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,求使
上的一个动点,求使![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)抛物线的解析式为![]() ,直线的解析式为
,直线的解析式为![]() .(2)
.(2)![]() ;(3)
;(3)![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)先把点A,C的坐标分别代入抛物线解析式得到a和b,c的关系式,再根据抛物线的对称轴方程可得a和b的关系,再联立得到方程组,解方程组,求出a,b,c的值即可得到抛物线解析式;把B、C两点的坐标代入直线y=mx+n,解方程组求出m和n的值即可得到直线解析式;
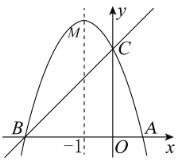
(2)设直线BC与对称轴x=-1的交点为M,此时MA+MC的值最小.把x=-1代入直线y=x+3得y的值,即可求出点M坐标;
(3)设P(-1,t),又因为B(-3,0),C(0,3),所以可得BC2=18,PB2=(-1+3)2+t2=4+t2,PC2=(-1)2+(t-3)2=t2-6t+10,再分三种情况分别讨论求出符合题意t值即可求出点P的坐标.
(1)依题意得: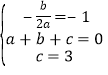 ,解得:
,解得: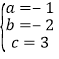 ,
,
∴抛物线的解析式为![]() .
.
∵对称轴为![]() ,且抛物线经过
,且抛物线经过![]() ,
,
∴把![]() 、
、![]() 分别代入直线
分别代入直线![]() ,
,
得![]() ,解之得:
,解之得:![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
(2)直线![]() 与对称轴
与对称轴![]() 的交点为
的交点为![]() ,则此时
,则此时![]() 的值最小,把
的值最小,把![]() 代入直线
代入直线![]() 得
得![]() ,
,
∴![]() .即当点
.即当点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小时
的距离之和最小时![]() 的坐标为
的坐标为![]() .
.
(注:本题只求![]() 坐标没说要求证明为何此时
坐标没说要求证明为何此时![]() 的值最小,所以答案未证明
的值最小,所以答案未证明![]() 的值最小的原因).
的值最小的原因).
(3)设![]() ,又
,又![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
①若点![]() 为直角顶点,则
为直角顶点,则![]() ,即:
,即:![]() 解得:
解得:![]() ,
,
②若点![]() 为直角顶点,则
为直角顶点,则![]() ,即:
,即:![]() 解得:
解得:![]() ,
,
③若点![]() 为直角顶点,则
为直角顶点,则![]() ,即:
,即:![]() 解得:
解得:
![]() ,
,![]() .
.
综上所述![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,数
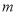 所对应的点与原点的距离叫做数
所对应的点与原点的距离叫做数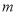 的绝对值,记作
的绝对值,记作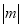
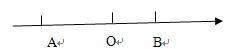
提出问题:(1)点
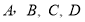 所表示的数如图所示,则
所表示的数如图所示,则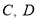 两点间的距离是 ,
两点间的距离是 , 两点间的距离是_____,
两点间的距离是_____,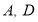 两点间的距离是 .
两点间的距离是 .探究结论:(2)在数轴上,若
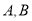 两点对应的数分别是
两点对应的数分别是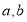 ,则
,则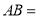 ____ (用含有
____ (用含有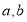 的式子表示).
的式子表示).拓展应用:(3)请利用.上述结论,解决下列问题:
①
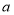 和
和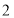 在数轴上对应的点之间的距离为
在数轴上对应的点之间的距离为 ②
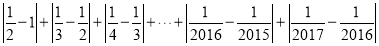
③满足
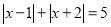 的未知数的值为
的未知数的值为 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=﹣3是关于x的方程(k+3)x+2=3x﹣2k的解.
(1)求k的值;
(2)在(1)的条件下,已知线段AB=6cm,点C是直线AB上一点,且BC=kAC,若点D是AC的中点,求线段CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若点A在数轴上对应的数为
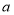 ,点B在数轴上对应的数为b,且
,点B在数轴上对应的数为b,且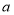 ,b满足
,b满足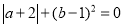
(1)求线段AB的长;
(2)点C在数轴上对应的数为x,且x是方程
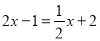 的解,在数轴上是否存在点P,使得PA+PB=PC?若存在,求出点P对应的数;若不存在,说明理由;
的解,在数轴上是否存在点P,使得PA+PB=PC?若存在,求出点P对应的数;若不存在,说明理由;(3)在(1)(2)条件下,点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒4个单位长度和9个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,请问:AB﹣BC的值是否随时间t的变化而改变?若变化,请说明理由;若不变,请求其常数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C在⊙O上,AD垂直于过点C的切线,垂足为D,且∠BAD=80°,则∠DAC的度数是_____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(1,
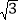 ),B(2,0),C点在x轴上运动,过点O作直线AC的垂线,垂足为D.当点C在x轴上运动时,点D也随之运动.则线段BD长的最大值为______________.
),B(2,0),C点在x轴上运动,过点O作直线AC的垂线,垂足为D.当点C在x轴上运动时,点D也随之运动.则线段BD长的最大值为______________. 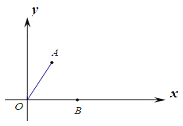
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业500名员工参加安全生产知识测试,成绩记为A,B,C,D,E共5个等级,为了解本次测试的成绩(等级)情况,现从中随机抽取部分员工的成绩(等级),统计整理并制作了如下的统计图:
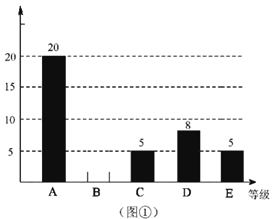
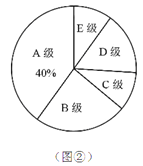
(1)求这次抽样调查的样本容量,并补全图①;
(2)如果测试成绩(等级)为A,B,C级的定为优秀,请估计该企业参加本次安全生产知识测试成绩(等级)达到优秀的员工的总人数.
相关试题

