【题目】如图,D是给定△ABC边BC所在直线上一动点,E是线段AD上一点,DE=2AE,连接BE,CE,点D从B的左边开始沿着BC方向运动,则△BCE的面积变换情况是( )
A.逐渐变大
B.逐渐变小
C.先变小后变大
D.始终不变
参考答案:
【答案】D
【解析】解:如图,过点E作EF⊥BC于F,过点A作AG⊥BC于G,
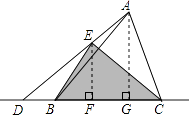
则EF∥AG,
所以,△ADG∽△EDF,
所以, ![]() =
= ![]() ,
,
∵DE=2AE,
∴AD=DE+AE=3AE,
∴ ![]() =
= ![]() ,
,
∴EF= ![]() AG,
AG,
∴△BCE的面积= ![]() BCEF=
BCEF= ![]() BC
BC ![]() AG=
AG= ![]() ×
× ![]() BCAG=
BCAG= ![]() S△ABC,
S△ABC,
∴△BCE的面积始终不变.
故答案为:D.
观察图形,△BCE和△ABC由公共边BC,只需找到这两个三角形BC边上的高之间的关系,即可求解。过点E作EF⊥BC于F,过点A作AG⊥BC于G,先证明△ADG∽△EDF,得到两条高之间的数量关系,再求出两三角形之间的面积关系即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为
 的正方形中,剪去一个边长为
的正方形中,剪去一个边长为 的小正方形(
的小正方形( ),将余下的部分拼成一个梯形,根据两个图形中阴影部分面积关系,解决下列问题:
),将余下的部分拼成一个梯形,根据两个图形中阴影部分面积关系,解决下列问题:(1)如图①所示,阴影部分的面积为 (写成平方差形式).

(2)如图②所示,梯形的上底是 ,下底是 ,高是 ,根据梯形面积公式可以算出面积是 (写成多项式乘法的形式).

(3)根据前面两问,可以得到公式 .
(4)运用你所得到的公式计算:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家商场同时出售同样的水瓶和水杯,且定价相同,请根据图中提供的信息,回答下列问题:

(1)一个水瓶与一个水杯分别是多少元?(请列方程解应用题)
(2)为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若某单位想要买5个水瓶和12个水杯,请问选择哪家商场购买更合算,并说明理由(水瓶和水杯必须在同一家购买).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器超市销售每台进价为120元、170元的A,B两种型号的电风扇,如表所示是近2周的销售情况:(进价、售价均保持不变,利润=销售收入一进货成本)
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
6
5
2200元
第二周
4
10
3200元
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市再采购这两种型号的电风扇共130台,并且全部销售完,该超市能否实现这两批的总利润为8010元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用完全平方公式因式分解在数学中的应用,请回答下列问题:
(1)因式分解:
 _______.
_______.(2)填空:
①当
 时,代数式
时,代数式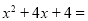 _______.
_______.②当
 _______时,代数式
_______时,代数式 ;
;③代数式
 的最小值是_______.
的最小值是_______.(3)拓展与应用:当
 、
、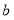 为何值时,代数式
为何值时,代数式 有最小值,并求出这个最小值.
有最小值,并求出这个最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,同学们探究下面命题的正确性,顶角为36°的等腰三角形我们称之为黄金三角形,“黄金三角形“具有一种特性,即经过它某一顶点的一条直线可以把它分成两个小等腰三角形,为此,请你,解答问题:
(1)已知如图1:黄金三角形△ABC中,∠A=36°,直线BD平分∠ABC交AC于点D,求证:△ABD和△DBC都是等腰三角形;

(2)如图,在△ABC中,AB=AC,∠A=36°,请你设计三种不同的方法,将△ABC分割成三个等腰三角形,不要求写出画法,不要求证明,但是要标出所分得的每个三角形的各内角的度数.
(3)已知一个三角形可以被分成两个等腰三角形,若原三角形的一个内角为36°,求原三角形的最大内角的所有可能值.




-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某游乐场的摩天轮(圆形转盘)上的点距离地面最大高度为160米,转盘直径为153米,旋转一周约需30分钟.某人从该摩天轮上到地面距离最近的点登舱,逆时针旋转20分钟,此时,他离地面的高度是米.

相关试题

