【题目】△ABC中,AB=AC=10,BC=12,矩形DEFG中,EF=4,FG>12.
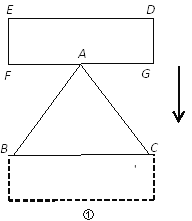
(1)如图①,点A是FG的中点,FG∥BC,将矩形DEFG向下平移,直到DE与BC重合为止.要研究矩形DEFG与△ABC重叠部分的面积,就要进行分类讨论,你认为如何进行分类,写出你的分类方法(无需求重叠部分的面积).
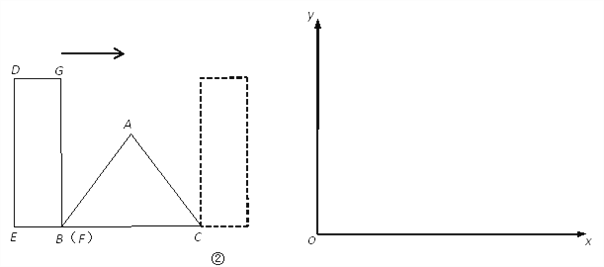
(2)如图②,点B与F重合,E、B、C在同一直线上,将矩形DEFG向右平移,直到点E与C重合为止.设矩形DEFG与△ABC重叠部分的面积为y,平移的距离为x.
① 求y与x的函数关系式,并写出自变量的取值范围;
② 在给定的平面直角坐标系中画出y与x的大致图象,并在图象上标注出关键点坐标.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)从重叠部分的形状看分为2类,即三角形和四边形(梯形);也可从数量的角度来分类,设平移的距离为x.分为0<x≤4,4<x≤8,8<x≤12三类等;
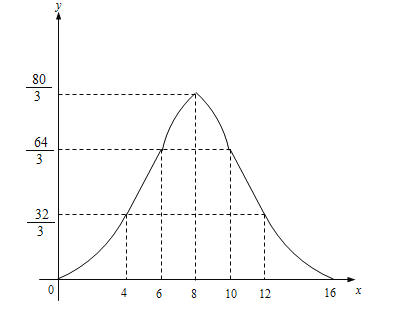
(2)①分类讨论:当0≤x≤4时;当4<x≤6时;当6<x≤10时;当10<x≤12时;当12<x≤16时,分别求出函数解析式;
②根据函数解析式,画出函数图象.
试题解析:(1)从重叠部分的形状看分为2类,即三角形和四边形(梯形);
也可从数量的角度来分类,设平移的距离为x.分为0<x≤4,4<x≤8,8<x≤12三类等;
(2)①当0≤x≤4时,y=![]() x2;
x2;
当4<x≤6时,y=![]() x-
x-![]() ;
;
当6<x≤10时,y=-![]() (x-8)2+
(x-8)2+![]() ;
;
当10<x≤12时,y=-![]() x+
x+![]() ;
;
当12<x≤16时,y=![]() (16-x)2.
(16-x)2.
②如图:
-
科目: 来源: 题型:
查看答案和解析>>【题目】有20筐白菜,以每筐
 为标准,超过和不足的千克数分别用正、负数来表示,记录如下:
为标准,超过和不足的千克数分别用正、负数来表示,记录如下:与标准质量的差值(单位:
 )
)


0
1
2.5
筐数
1
4
2
3
2
8
(1)20筐白菜中,最重的一筐比最轻的一筐重
 ;
;(2)与标准质量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价1.68元,则出售这20筐白菜一共可卖多少元?(结果保留整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察图,回答下列问题

(1)在图①中有几个角?
(2)在图②中有几个角?
(3)在图③中有几个角?
(4)以此类推,如图④所示,若一个角有n条射线,此时共有多少个角?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系网格中,三角形
 的顶点坐标分别是
的顶点坐标分别是 .将三角形
.将三角形 平移,使顶点
平移,使顶点 平移到坐标原点
平移到坐标原点 处,得到三角形
处,得到三角形 .
.(1)
 的坐标是________,
的坐标是________, 的坐标是________.
的坐标是________.(2)画出平移后的
 .
.(3)求
 的面积。
的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了庆祝祖国70岁生日,阳光中学举行“向祖国70岁生日献礼”系列活动。学校团委为了组织好大型团体操表演,随机抽查部分七年级学生的身高,将学生身高分成四个组,并绘制成如下不完整的统计图表。
组别
身高
人数
1组
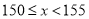
15
2组
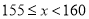
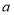
3组
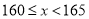
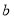
4组
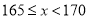
10
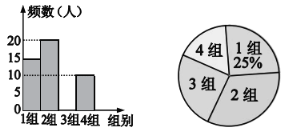
根据以上信息,解答下列问题:
(1)在统计表中,
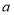 的值是________;本次调查的学生人数是________人.
的值是________;本次调查的学生人数是________人.(2)补全频数分布直方图.
(3)在“祖国万岁”方队中,列队形成“祖国”二字学生的身高应该在
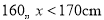 的范围,该校七年级480名学生中,身高符合该条件的学生约有多少人?
的范围,该校七年级480名学生中,身高符合该条件的学生约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,一次函数y1=x+2与反比例函数y2=
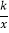 (x>0)的图象交于点A(a,5)
(x>0)的图象交于点A(a,5)(1)确定反比例函数的表达式;
(2)结合图象,直接写出x为何值时,y1<y2
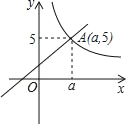
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下图,填空:

(1)第n个图形中有多少个“
 ” 和“☆”?
” 和“☆”?(2)第n个图形有182个“
 ” 该图形中有多少个“☆”?
” 该图形中有多少个“☆”?
相关试题

