【题目】已知:如图,⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.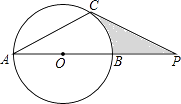
(1)求证:CP是⊙O的切线;
(2)若PC=6,AB=4 ![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
参考答案:
【答案】
(1)解:如图,连接OC;
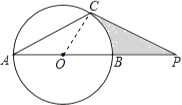
∵OA=OC,AC=CP,
∴∠A=∠OCA=30°,∠P=∠A=30°,
∴∠POC=∠A+∠OCA=60°,
∴∠OCP=180°﹣60°﹣30°=90°,
∴CP是⊙O的切线.
(2)解:∵AB=4 ![]() ,
,
∴OC=OB=2 ![]() ,
,
∴ ![]()
= ![]() ×
× ![]() =6
=6 ![]() ,
,
![]() =2π,
=2π,
∴图中阴影部分的面积=6 ![]() ﹣2π.
﹣2π.
【解析】(1)连接OC;由等边对等角得出∠A=∠OCA=30°,∠P=∠A=30°,利用三角形的外角得出∠POC=∠A+∠OCA=60°,进而根据三角形的内角和得出∠OCP=180°﹣60°﹣30°=90°,从而得出结论;(2)由三角形的面积公式得出S △ O C P = ![]() O C P C,由扇形面积公式得出S扇形OBC=2π,图中阴影部分的面积=S △ O C P-S扇形OBC计算即可。
O C P C,由扇形面积公式得出S扇形OBC=2π,图中阴影部分的面积=S △ O C P-S扇形OBC计算即可。
【考点精析】掌握切线的判定定理和扇形面积计算公式是解答本题的根本,需要知道切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知k1<0<k2 , 则函数b=﹣1<0∴和y=
 的图象大致是( )
的图象大致是( )
A.
B.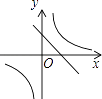
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为平行四边形ABCD边AD上一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S、S1、S2 , 若S=2,则S1+S2=( )
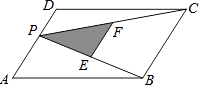
A.4
B.6
C.8
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c>0;
④当y>0时,x的取值范围是﹣1≤x<3;
⑤当x<0时,y随x增大而增大;
其中结论正确有 .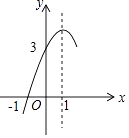
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(2,1),B(2,4).
(1)若直线l:y=x+b与AB有一个交点.

则b的取值范围为_______________;
(2)若直线l:y=kx与AB有一个交点.
则k的取值范围为_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F,若AF=6,则四边形AEDF的周长是( )

A. 24 B. 28 C. 32 D. 36
-
科目: 来源: 题型:
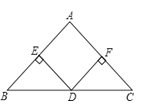
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,∠A=90°,点D是BC边上的中点,DE⊥AB于点E,DF⊥AC于点F.求证:四边形AEDF是正方形.
相关试题

