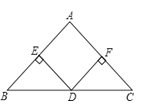
【题目】如图,在等腰Rt△ABC中,∠A=90°,点D是BC边上的中点,DE⊥AB于点E,DF⊥AC于点F.求证:四边形AEDF是正方形.
参考答案:
【答案】见详解
【解析】
由于AB=AC,那么∠B=∠C,而DE⊥AB,DF⊥AC可知∠BED=∠CFD=90°,又∵D是BC中点,可知BD=CD,利用AAS可证△BED≌△CFD,从而有DE=DF.再由∠AED=∠AFD=∠A=90°可知四边形AEDF为矩形,从而可得四边形AEDF为正方形.
证明:∵在等腰Rt△ABC中,∠A=90°,
∴AB=AC,
∴∠B=∠C,
又∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=∠AED=∠AFD=90°,
又∵D是BC中点,
∴BD=CD,
在△BED与△CFD中,
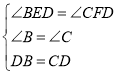
∴△BED≌△CFD(AAS),
∴DE=DF.
∵∠A=∠AED=∠AFD=90°
∴四边形AEDF为矩形,
又∵DE=DF,
∴矩形AEDF为正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.
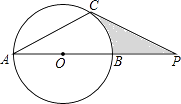
(1)求证:CP是⊙O的切线;
(2)若PC=6,AB=4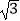 ,求图中阴影部分的面积.
,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(2,1),B(2,4).
(1)若直线l:y=x+b与AB有一个交点.

则b的取值范围为_______________;
(2)若直线l:y=kx与AB有一个交点.
则k的取值范围为_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F,若AF=6,则四边形AEDF的周长是( )

A. 24 B. 28 C. 32 D. 36
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
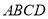 中,把矩形
中,把矩形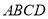 绕点
绕点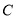 旋转,得到矩形
旋转,得到矩形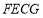 ,且点
,且点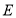 落在
落在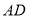 上,连接
上,连接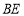 ,
,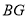 ,
,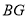 交
交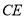 于点
于点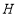 ,连接
,连接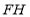 ,若
,若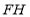 平分
平分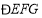 ,则下列结论:
,则下列结论:①
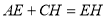 ;
;②
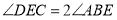 ;
;③
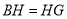 ;
;④
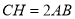 ,其中正确的个数是( )
,其中正确的个数是( )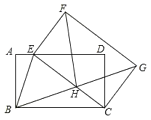
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),……,那么点A2019的坐标为( )
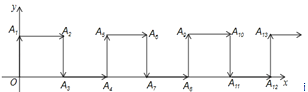
A.(1008,1)B.(1009,1)C.(1009,0)D.(1010,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料解决问题:
材料:古希腊著名数学家 毕达哥拉斯发现把数1,3,6,10,15,21…这些数量的(石子),都可以排成三角形,则称像这样的数为三角形数.
把数 1,3,6,10,15,21…换一种方式排列,即
1=1
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5=15
…
从上面的排列方式看,把1,3,6,10,15,…叫做三角形数“名副其实”.
(1)设第一个三角形数为a1=1,第二个三角形数为a2=3,第三个三角形数为a3=6,请直接写出第n个三角形数为an的表达式(其中n为正整数).
(2)根据(1)的结论判断66是三角形数吗?若是请说出66是第几个三角形数?若不是请说明理由.
(3)根据(1)的结论判断所有三角形数的倒数之和T与2的大小关系并说明理由.
相关试题

