搜索
【题目】如图，△ABC中，AD平分∠BAC，DE∥AC交AB于E，DF∥AB交AC于F，若AF=6，则四边形AEDF的周长是（ ）
A. 24 B. 28 C. 32 D. 36
参考答案：
【答案】A
【解析】根据DE∥AC、DF∥AB即可得出四边形AEDF为平行四边形，再根据AD平分∠BAC即可得出∠FAD=∠FDA，即FA=FD，从而得出平行四边形AEDF为菱形，根据菱形的性质结合AF=6即可求出四边形AEDF的周长．
∵DE∥AC,DF∥AB，
∴四边形AEDF为平行四边形,∠EAD=∠FDA.
∵AD平分∠BAC，
∴∠EAD=∠FAD=∠FDA，
∴FA=FD，
∴平行四边形AEDF为菱形。
∵AF=6，
∴菱形AEDF的周长=4AF=4×6=24.
故选A.
-
科目： 来源： 题型：
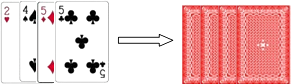
查看答案和解析>>【题目】如图，甲、乙用4张扑克牌玩游戏，他俩将扑克牌洗匀后背面朝上，放置在桌面上，每人抽一张，甲先抽，乙后抽，抽出的牌不放回．甲、乙约定：只有甲抽到的牌面数字比乙大时甲胜；否则乙胜．请你用树状图或列表法说明甲、乙获胜的机会是否相同．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一块直角三角形的纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于（ ）.
A. 2 cm B. 4 cm C. 3 cm D. 5 cm
-
科目： 来源： 题型：
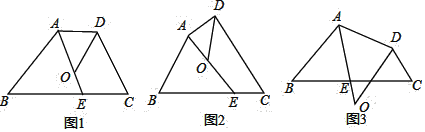
查看答案和解析>>【题目】四边形ABCD中，∠BAD的角平分线与边BC交于点E，∠ADC的角平分线交直线AE于点O．
（1）若点O在四边形ABCD的内部，
①如图1，若AD∥BC，∠B=40°，∠C=70°，则∠DOE= °；
②如图2，试探索∠B、∠C、∠DOE之间的数量关系，并将你的探索过程写下来．
（2）如图3，若点O在四边形ABCD的外部，请你直接写出∠B、∠C、∠DOE之间的数量关系．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，AB=15，AC=13，BC边上的高AD=12，则BC的长为________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中，恰好四个顶点都在横格线上，已知∠α=36°，求长方形卡片的周长．（精确到1mm）（参考数据：sin36°≈0.60，cos36°≈0.80，tan36°≈0.75）
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义正整数m，n的运算，m△n＝
例2△3＝
，3△4＝
（1）3△2的值为 运算符号“△”满足交换律吗？回答 （填“是”或者“否”）
（2）探究：计算2△10＝
的值．为解决上面的问题，我们运用数形结合的思想方法，通过不断的分割一个面积为1的正方形，把数量关系和几何图形结合起来，最终解决问题．
如图所示，第1次分割把正方形的面积二等分，其中阴影部分的面积为
，第2次，把上次分割图中空白部分的面积继续二等分，阴影分的面积之和为
，第3次分割把上次分割图中空白部分的面积继续二等分……以此类推……第10次分割，把第9次分割后的图中的空日部分的面积最后二等分，所有阴影部分面积之和为．根据第10次分割图可以得出计结果：
＝1﹣
，进一步分析可得出
＝1﹣
，
（3）已知n是正整数，计算3×（4△n）＝
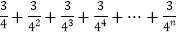的结果．按指定方法解决问题请仿照以上做法，只需画出第n次分割图并作标注，写出最终结果的推理步骤，或借用以上结论进行推理，写出必要的步骤．
相关试题
