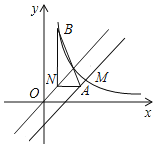
【题目】如图,一次函数y=x﹣2与反比例函数y=![]() (x>0)的图象相交于点M(m,1).
(x>0)的图象相交于点M(m,1).
(1)填空:m的值为 ,反比例函数的解析式为 ;
(2)已知点N(n,n),过点N作l1∥x轴,交直线y=x﹣2于点A,过点N作l2∥y轴,交反比例函数y=![]() (x>0)的图象与点B,试用n表示△NAB的面积S.
(x>0)的图象与点B,试用n表示△NAB的面积S.

参考答案:
【答案】(1)3,y=![]() ;(2)|
;(2)|![]() ﹣n|.
﹣n|.
【解析】分析:(1)把M(m,1)代入一次函数y=x-2,可得m的值;把M(3,1)代入反比例函数y=![]() (x>0),可得k的值;
(x>0),可得k的值;
(2)依据点N与点A的纵坐标相同,均为n,可得AN=n+2-n=2,依据点N与点B的横坐标相同,均为n,可得BN=|![]() -n|,即可得到S△NBA=
-n|,即可得到S△NBA=![]() ×2×|
×2×|![]() -n|=|
-n|=|![]() -n|.
-n|.
详解:(1)把M(m,1)代入一次函数y=x-2,可得
1=m-2,
解得m=3,
把M(3,1)代入反比例函数y=![]() (x>0),可得
(x>0),可得
k=3×1=3,
∴反比例函数的解析式为y=![]() ,
,
(2)由题可得,点N与点A的纵坐标相同,均为n,
将y=n代入y=x-2中,得x=n+2,
∴A(n+2,n),
∴AN=n+2-n=2,
由题可得,点N与点B的横坐标相同,均为n,
将x=n代入y=![]() 中,得y=
中,得y=![]() ,
,
∴B(n,![]() ),
),
∴BN=|![]() -n|,
-n|,
∴S△NBA=![]() ×2×|
×2×|![]() -n|=|
-n|=|![]() -n|.
-n|.
-
科目: 来源: 题型:
查看答案和解析>>【题目】开学初,李芳和王平去文具店购买学习用品,李芳用18元钱买了1支钢笔和3本笔记本;王平用30元买了同样的钢笔2支和笔记本4本.
(1)求每支钢笔和每本笔记本的价格;
(2)校运会后,班主任拿出200元学校奖励基金交给班长,购买上述价格的钢笔笔记本共36件作为奖品,奖给校运会中表现突出的同学,要求笔记本数不多于钢笔数的2倍,共有多少种购买方案?请你一一写出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】同时抛掷A,B两个均匀的小立方体(每个面上分别标有数字1,2,3,4,5,6),设两立方体朝上的数字分别为x,y,并以此确定点P(x,y),那么点P落在直线y=-2x+9上的概率为( )
A.
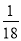 B.
B. 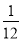 C.
C. 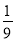 D.
D. 
-
科目: 来源: 题型:
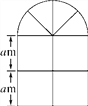
查看答案和解析>>【题目】(12分)如图是某种窗户的形状,其上部是半圆形,下部是边长相同的四个小正方形,已知下部的小正方形的边长为am,计算:
(1)窗户的面积;
(2)窗框的总长;
(3)若a=1,窗户上安装的是玻璃,玻璃每平方米25元,窗框每米20元,窗框的厚度不计,求制作这种窗户需要的费用是多少元(π取3.14,结果保留整数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图, AF平分∠BAC,BC⊥AF, 垂足为E,点D与点A关于点E对称,PB分别与线段CF,AF相交于P,M.

(1)求证:AB=CD;
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
-
科目: 来源: 题型:
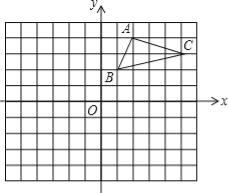
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标.
【答案】(1)作图见解析;点A1的坐标(2,﹣4);(2)作图见解析;点A2的坐标(﹣2,4).
【解析】
试题分析:(1)分别找出A、B、C三点关于x轴的对称点,再顺次连接,然后根据图形写出A点坐标;
(2)将△A1B1C1中的各点A1、B1、C1绕原点O旋转180°后,得到相应的对应点A2、B2、C2,连接各对应点即得△A2B2C2.
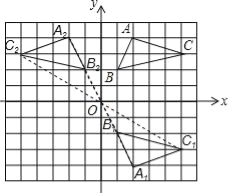
试题解析:(1)如图所示:点A1的坐标(2,﹣4);
(2)如图所示,点A2的坐标(﹣2,4).
考点:1.作图-旋转变换;2.作图-轴对称变换.
【题型】解答题
【结束】
18【题目】观察下面的点阵图和相应的等式,探究其中的规律:
(1)认真观察,并在④后面的横线上写出相应的等式.
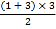
①1=1 ②1+2=
 =3 ③1+2+3=
=3 ③1+2+3=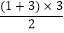 =6 ④ …
=6 ④ …(2)结合(1)观察下列点阵图,并在⑤后面的横线上写出相应的等式.

1=12②1+3=22③3+6=32④6+10=42⑤ …
(3)通过猜想,写出(2)中与第n个点阵相对应的等式 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个多项式A=9xy+7xy-x-2,B=3xy-5xy+x+7
(1)求A-3B;
(2)若要使A-3B的值与x的取值无关,试求y的值;
相关试题

