【题目】已知:如图, AF平分∠BAC,BC⊥AF, 垂足为E,点D与点A关于点E对称,PB分别与线段CF,AF相交于P,M.

(1)求证:AB=CD;
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
参考答案:
【答案】(1)证明见解析;(2)∠F=∠MCD,理由见解析.
【解析】
(1)根据全等三角形的性质和判定和线段垂直平分线性质求出AB=AC=CD,
(2)由AB=AC=CD推出∠CDA=∠CAD=∠CPM,求出∠MPF=∠CDM,∠PMF=∠BMA=∠CMD,在△DCM和△PMF中根据三角形的内角和定理求出即可.
(1)∵AF平分∠BAC,BC⊥AF,
∴∠CAE=∠BAE,∠AEC=∠AEB=90°,
在△ACE和△ABE中,∵∠AEC=∠AEB,AE=AE,∠CAE=∠BAE,
∴△ACE≌△ABE(ASA),
∴AB=AC,
∵∠CAE=∠CDE,
∴AM是BC的垂直平分线,
∴CM=BM,CE=BE,
∴∠CMA=∠BMA,
∵AE=ED,CE⊥AD,
∴AC=CD,
∴AB=CD;
(2)∠F=∠MCD,
理由是:∵AC=CD,
∴∠CAD=∠CDA,
∵∠BAC=2∠MPC,
又∵∠BAC=2∠CAD,
∴∠MPC=∠CAD,
∴∠MPC=∠CDA,
∴∠MPF=∠CDM,
∴∠MPF=∠CDM(等角的补角相等),
∵∠DCM+∠CMD+∠CDM=180°,∠F+∠MPF+∠PMF=180°,
又∵∠PMF=∠BMA=∠CMD,
∴∠MCD=∠F.
-
科目: 来源: 题型:
查看答案和解析>>【题目】同时抛掷A,B两个均匀的小立方体(每个面上分别标有数字1,2,3,4,5,6),设两立方体朝上的数字分别为x,y,并以此确定点P(x,y),那么点P落在直线y=-2x+9上的概率为( )
A.
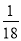 B.
B. 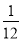 C.
C. 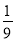 D.
D. 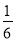
-
科目: 来源: 题型:
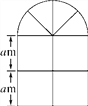
查看答案和解析>>【题目】(12分)如图是某种窗户的形状,其上部是半圆形,下部是边长相同的四个小正方形,已知下部的小正方形的边长为am,计算:
(1)窗户的面积;
(2)窗框的总长;
(3)若a=1,窗户上安装的是玻璃,玻璃每平方米25元,窗框每米20元,窗框的厚度不计,求制作这种窗户需要的费用是多少元(π取3.14,结果保留整数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=x﹣2与反比例函数y=
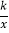 (x>0)的图象相交于点M(m,1).
(x>0)的图象相交于点M(m,1).(1)填空:m的值为 ,反比例函数的解析式为 ;
(2)已知点N(n,n),过点N作l1∥x轴,交直线y=x﹣2于点A,过点N作l2∥y轴,交反比例函数y=
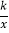 (x>0)的图象与点B,试用n表示△NAB的面积S.
(x>0)的图象与点B,试用n表示△NAB的面积S.
-
科目: 来源: 题型:
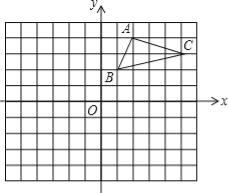
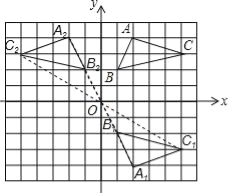
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标.
【答案】(1)作图见解析;点A1的坐标(2,﹣4);(2)作图见解析;点A2的坐标(﹣2,4).
【解析】
试题分析:(1)分别找出A、B、C三点关于x轴的对称点,再顺次连接,然后根据图形写出A点坐标;
(2)将△A1B1C1中的各点A1、B1、C1绕原点O旋转180°后,得到相应的对应点A2、B2、C2,连接各对应点即得△A2B2C2.
试题解析:(1)如图所示:点A1的坐标(2,﹣4);
(2)如图所示,点A2的坐标(﹣2,4).
考点:1.作图-旋转变换;2.作图-轴对称变换.
【题型】解答题
【结束】
18【题目】观察下面的点阵图和相应的等式,探究其中的规律:
(1)认真观察,并在④后面的横线上写出相应的等式.
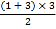
①1=1 ②1+2=
 =3 ③1+2+3=
=3 ③1+2+3=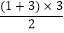 =6 ④ …
=6 ④ …(2)结合(1)观察下列点阵图,并在⑤后面的横线上写出相应的等式.

1=12②1+3=22③3+6=32④6+10=42⑤ …
(3)通过猜想,写出(2)中与第n个点阵相对应的等式 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个多项式A=9xy+7xy-x-2,B=3xy-5xy+x+7
(1)求A-3B;
(2)若要使A-3B的值与x的取值无关,试求y的值;
-
科目: 来源: 题型:
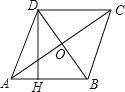
查看答案和解析>>【题目】如图,四边形ABCD是菱形,对角线AC和BD相交于点O,AC=8cm,BD=6cm,DH⊥AB于H.
(1)求菱形ABCD的面积;
(2)求DH的长.
相关试题

