【题目】解方程:
(1)5x+6=2x﹣3
(2)2x﹣3(x﹣1)=7
(3)![]()
(4)![]()
参考答案:
【答案】(1)x=﹣3;(2)x=﹣4;(3)x=﹣1;(4)x=![]()
【解析】
(1)移项、合并同类项、系数化为1,据此求出方程的解即可.
(2)去括号、移项、合并同类项、系数化为1,据此求出方程的解即可.
(3)去分母、去括号、移项、合并同类项、系数化为1,据此求出方程的解即可.
(4)去分母、去括号、移项、合并同类项、系数化为1,据此求出方程的解即可.
(1)移项,合并同类项,可得:3x=﹣9,
系数化为1,得:x=﹣3.
(2)去括号,得:2x﹣3x+3=7
移项,得:2x﹣3x=7﹣3
合并同类项,得:﹣x=4
系数化为1,得:x=﹣4
(3)去分母,得:6x﹣3(x﹣1)=12﹣2(x+7)
去括号,得:6x﹣3x+3=12﹣2x﹣14
移项,得:6x﹣3x+2x=12﹣14﹣3
合并同类项,得:5x=﹣5
系数化为1,得:x=﹣1
(4)两边同时乘以6,去分母,得:30(0.5x﹣1)﹣20(0.1x+2)=﹣6
去括号,得:15x﹣30﹣2x﹣40=﹣6
移项,得:15x﹣2x=﹣6+30+40
合并同类项,得:13x=64
系数化为1,得:x=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.

根据以上信息解决下列问题:
(1)
 ,
, ;
;(2)扇形统计图中机器人项目所对应扇形的圆心角度数为
 ;
;(3)从选航模项目的
 名学生中随机选取
名学生中随机选取 名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的
名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的 名学生中恰好有
名学生中恰好有 名男生、
名男生、 名女生的概率.
名女生的概率. -
科目: 来源: 题型:
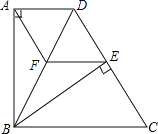
查看答案和解析>>【题目】如图,四边形ABCD中,AD∥BC,BA⊥AD,BC=DC,BE⊥CD于点E.
(1)求证:△ABD≌△EBD;
(2)过点E作EF∥DA,交BD于点F,连接AF.求证:四边形AFED是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,小明在大楼的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡角∠ABC=30°点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
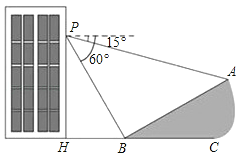
(1)山坡AB的坡度为 ;
(2)若山坡AB的长为20米,求大楼的窗口P处距离地面的高度.
-
科目: 来源: 题型:
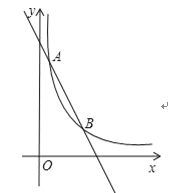
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数
 的图象交于点A(1,6),B(3,n)两点.
的图象交于点A(1,6),B(3,n)两点.(1)求一次函数的表达式;
(2)在y轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标平面内,小明站在点A(﹣10,0)处观察y轴,眼睛距地面1.5米,他的前方5米处有一堵墙DC,若墙高DC=2米,则小明在y轴上的盲区(即OE的长度)为_____米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=﹣x2+bx+3的图象与x轴交于A、C两点(点A在点C的左侧),与y轴交于点B,且OA=OB.
(1)求线段AC的长度;
(2)若点P在抛物线上,点P位于第二象限,过P作PQ⊥AB,垂足为Q.已知PQ=
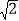 ,求点P的坐标.
,求点P的坐标.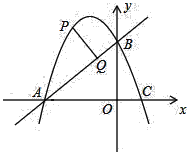
相关试题

