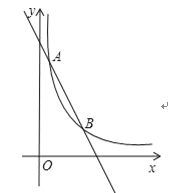
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图象交于点A(1,6),B(3,n)两点.
的图象交于点A(1,6),B(3,n)两点.
(1)求一次函数的表达式;
(2)在y轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
参考答案:
【答案】(1)y=-2x+8 ;(2)P(0,5) 3
【解析】试题分析:(1)将A点坐标代入反比例函数解析式即可求出m的值,再将x=3代入反比例函数解析式解得n的值,由此得出B点的坐标,结合A、B两点的坐标,利用待定系数法即可求出一次函数的表达式;
(2)作点A关于y轴的对称点A′,连接A′B交y轴于点P,在y轴上任选一点不同于P点的P′点,由三角形内两边之和大于第三边来验证点P就是我们找到的使得PA+PB的值最小的点,由A点的坐标找出点A′的坐标,由待定系数法可求出直线A′B的函数表达式,令x=0即可得出P点的坐标;再结合三角形的面积公式与点到直线的距离即可求出△PAB的面积.
试题解析:解:(1)将点A(1,6)代入反比例函数![]() 中,得6=
中,得6=![]() ,即m=6.
,即m=6.
故反比例函数的解析式为![]() .
.
∵点B(3,n)在反比例函数![]() 上,∴n=
上,∴n=![]() =2.即点B的坐标为(3,2).
=2.即点B的坐标为(3,2).
将点A(1,6)、点B(3,2)代入y=kx+b中,得: ![]() ,解得:
,解得: ![]() .
.
故一次函数的解析式为y=﹣2x+8.
(2)作点A关于y轴的对称点A′,连接A′B交y轴于点P,如图1所示.

在y轴上任取一点P′(不同于点P).∵A、A′关于y轴对称,∴AP=A′P,AP′=A′P′.在△P′A′B中,有A′P′+BP′=AP′+BP′>A′B=A′P+BP=AP+BP,∴当A′、P、B三点共线时,PA+PB最小.
∵点A的坐标为(1,6),∴点A′的坐标为(﹣1,6).
设直线A′B的解析式为y=ax+b,将点A′(﹣1,6)、点B(3,2)代入到y=ax+b中,得: ![]() ,解得:
,解得: ![]() ,∴直线A′B的解析式为y=﹣x+5,令x=0,则有y=5.
,∴直线A′B的解析式为y=﹣x+5,令x=0,则有y=5.
即点P的坐标为(0,5).
直线AB解析式为y=﹣2x+8,即2x+y﹣8=0.
AB=![]() =
=![]() ,点P到直线AB的距离d=
,点P到直线AB的距离d=![]() =
=![]() .
.
△PAB的面积S=![]() ABD=
ABD=![]() ×
×![]() ×
×![]() =3.
=3.
-
科目: 来源: 题型:
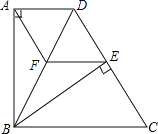
查看答案和解析>>【题目】如图,四边形ABCD中,AD∥BC,BA⊥AD,BC=DC,BE⊥CD于点E.
(1)求证:△ABD≌△EBD;
(2)过点E作EF∥DA,交BD于点F,连接AF.求证:四边形AFED是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,小明在大楼的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡角∠ABC=30°点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
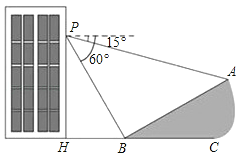
(1)山坡AB的坡度为 ;
(2)若山坡AB的长为20米,求大楼的窗口P处距离地面的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)5x+6=2x﹣3
(2)2x﹣3(x﹣1)=7
(3)
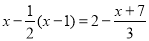
(4)
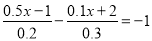
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标平面内,小明站在点A(﹣10,0)处观察y轴,眼睛距地面1.5米,他的前方5米处有一堵墙DC,若墙高DC=2米,则小明在y轴上的盲区(即OE的长度)为_____米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=﹣x2+bx+3的图象与x轴交于A、C两点(点A在点C的左侧),与y轴交于点B,且OA=OB.
(1)求线段AC的长度;
(2)若点P在抛物线上,点P位于第二象限,过P作PQ⊥AB,垂足为Q.已知PQ=
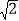 ,求点P的坐标.
,求点P的坐标.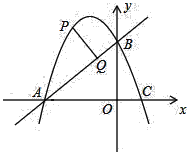
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下面四个结论:(1)AE=BF,(2)AE⊥BF,(3)AO=OE,(4)S△AOB=S四边形DEOF,其中正确结论的序号是 .

相关试题

