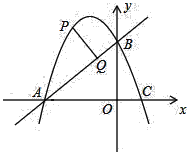
【题目】如图,已知二次函数y=﹣x2+bx+3的图象与x轴交于A、C两点(点A在点C的左侧),与y轴交于点B,且OA=OB.
(1)求线段AC的长度;
(2)若点P在抛物线上,点P位于第二象限,过P作PQ⊥AB,垂足为Q.已知PQ=![]() ,求点P的坐标.
,求点P的坐标.
参考答案:
【答案】(1)线段AC的长是4;(2)点P的坐标为(﹣2,3)或(﹣1,4).
【解析】
(1)根据题意可以求得点B的坐标,从而可得到点A的坐标,进而求得函数解析式,再令y=0,即可得到点C的坐标,从而可以得到线段AC的长;
(2)根据点A和点B的坐标可以得到直线AB的函数解析式,然后根据二次函数的性质和平行线的性质,可以求得点P的坐标,本题得以解决.
(1)∵二次函数y=﹣x2+bx+3的图象与y轴交于点B,且OA=OB,
∴点B的坐标为(0,3),∴OB=OA=3,
∴点A的坐标为(﹣3,0),∴0=﹣(﹣3)2+b×(﹣3)+3,解得,b=﹣2,
∴y=﹣x2﹣2x+3=﹣(x+3)(x﹣1),
∴当y=0时,x1=﹣3,x2=1,
∴点C的坐标为(1,0),∴AC=1﹣(﹣3)=4,
即线段AC的长是4;
(2)∵点A(﹣3,0),点B(3,0),
∴直线AB的函数解析式为y=x+3,
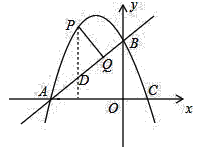
过点P作PD∥y轴交直线AB于点D,
设点P的坐标为(m,﹣m2﹣2m+3),则点D的坐标为(m,m+3),
∴PD=﹣m2﹣2m+3﹣(m+3)=﹣m2﹣3m,
∵PD∥y轴,∠ABO=45°,
∴∠PDQ=∠ABO=45°,
又∵PQ⊥AB,PQ=![]() ,
,
∴△PDQ是等腰直角三角形,
∴PD=![]() =2,∴﹣m2﹣3m=2,解得,m1=﹣1,m2=﹣2,
=2,∴﹣m2﹣3m=2,解得,m1=﹣1,m2=﹣2,
当m=﹣1时,﹣m2﹣2m+3=4,
当m=﹣2时,﹣m2﹣2m+3=3,
∴点P的坐标为(﹣2,3)或(﹣1,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)5x+6=2x﹣3
(2)2x﹣3(x﹣1)=7
(3)
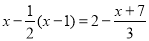
(4)
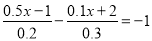
-
科目: 来源: 题型:
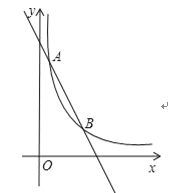
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数
 的图象交于点A(1,6),B(3,n)两点.
的图象交于点A(1,6),B(3,n)两点.(1)求一次函数的表达式;
(2)在y轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标平面内,小明站在点A(﹣10,0)处观察y轴,眼睛距地面1.5米,他的前方5米处有一堵墙DC,若墙高DC=2米,则小明在y轴上的盲区(即OE的长度)为_____米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下面四个结论:(1)AE=BF,(2)AE⊥BF,(3)AO=OE,(4)S△AOB=S四边形DEOF,其中正确结论的序号是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某文化用品商店用1 000元购进一批“晨光”套尺,很快销售一空;商店又用1 500元购进第二批该款套尺,购进时单价是第一批的
 倍,所购数量比第一批多100套.
倍,所购数量比第一批多100套.(1)求第一批套尺购进时单价是多少?
(2)若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式M=(a+b+1)x3+(2a﹣b)x2+(a+2b)x﹣4是关于x的二次多项式.
(1)若方程3(a+b)y=ky﹣8的解是y=4,求k的值;
(2)当x=2时,代数式M的值为﹣34.当x=﹣2时,求代数式M的值.
相关试题

