【题目】如图,已知∠A=∠AGE,∠D=∠DGC
(1)求证:AB∥CD;
(2)若∠1+∠2=180°,求证:∠BEC+∠B=180°;
(3)在(2)的基础上,若∠BEC=2∠B+30°,求∠C的度数.

参考答案:
【答案】(1)见解析;(2)见解析;(3)∠C=50°.
【解析】
(1)求出∠A=∠D,根据平行线的判定推出即可;
(2)求出∠2+∠BHA=180°,根据平行线的判定推出BF∥CE,根据平行线的性质得出即可;
(3)求出∠BEC的度数,根据平行线的性质求出即可.
(1)证明:∵∠A=∠AGE,∠D=∠DGC,
又∵∠AGE=∠DGC,
∴∠A=∠D,
∴AB∥CD;
(2)证明:∵∠1=∠BHA,∠1+∠2=180°,
∴∠2+∠BHA=180°,
∴BF∥CE,
∴∠BEC+∠B=180°;
(3)∵∠BEC+∠B=180°,∠BEC=2∠B+30°,
∴∠B=50°,∠BEC=130°,
∵AB∥CD,
∴∠C+∠BEC=180°,
∴∠C=50°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个不透明的口袋,甲口袋中装有3个分别标有数字1,2,3的小球,乙口袋中装有2 个分别标有数字4,5的小球,它们的形状、大小完全相同,现随机从甲口袋中摸出一个小球记下数字,再从乙口袋中摸出一个小球记下数字
(1)请用画树状图的方法表示出两次所得数字可能能出现的所有结果;
(2)求出两个数字之和能被2 整除的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBEF是菱形?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点P的坐标为(2a+6,a-3)
(1)当点P的纵坐标为-4,求a的值;
(2)若点P在y轴上,求点P的坐标;
(3)若点P在第四象限,求a的取值范围.
-
科目: 来源: 题型:
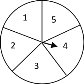
查看答案和解析>>【题目】如图,转盘中5个扇形的面积都相等,任意转动转盘一次,当转盘停止转动时,把下列事件:①指针落在标有3的区域内;②指针落在标有奇数的区域;③指针落在标有6的区域内;④指针落在标有偶数或奇数的区域,的序号按发生的可能性从小到大的顺序排列为_____.
-
科目: 来源: 题型:
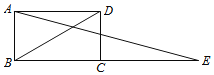
查看答案和解析>>【题目】如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ABD=m°,则∠E=_____度(用含m的代数式表示).
-
科目: 来源: 题型:
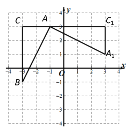
查看答案和解析>>【题目】如图,在平面直角坐标系中,有一Rt△ABC,∠C=90°且A(-1,3)、B(-3,-1)、C(-3,3),已知△A1AC1是由△ABC旋转得到的.若点Q在x轴上,点P在直线AB上,要使以Q、P、A1、C1为顶点的四边形是平行四边形,满足条件的点Q的坐标为______.
相关试题

