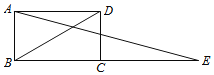
【题目】如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ABD=m°,则∠E=_____度(用含m的代数式表示).
参考答案:
【答案】45-![]() m
m
【解析】
连接AC,由矩形性质可得∠ABC=90°,AC=BD,OB=OC,继而可得∠OCB=∠OBC,∠E=∠CAE,由∠ABD=m°,可得∠OBC=90°-m°,再由三角形外角的性质即可求得答案.
连接AC,交BD于点O,
∵四边形ABCD是矩形,
∴∠ABC=90°,AC=BD,OB=OC,
∴∠OCB=∠OBC,
又∵BD=CE,
∴CE=CA,
∴∠E=∠CAE,
∵∠ABD=m°,
∴∠OBC=∠ABC-∠ABD=90°-m°,
∵∠OCB=∠CAE+∠E,
∴∠E+∠E=90°-m°,
∴∠E=(45-![]() m)°,
m)°,
故答案为:45-![]() m.
m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点P的坐标为(2a+6,a-3)
(1)当点P的纵坐标为-4,求a的值;
(2)若点P在y轴上,求点P的坐标;
(3)若点P在第四象限,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠A=∠AGE,∠D=∠DGC
(1)求证:AB∥CD;
(2)若∠1+∠2=180°,求证:∠BEC+∠B=180°;
(3)在(2)的基础上,若∠BEC=2∠B+30°,求∠C的度数.

-
科目: 来源: 题型:
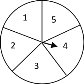
查看答案和解析>>【题目】如图,转盘中5个扇形的面积都相等,任意转动转盘一次,当转盘停止转动时,把下列事件:①指针落在标有3的区域内;②指针落在标有奇数的区域;③指针落在标有6的区域内;④指针落在标有偶数或奇数的区域,的序号按发生的可能性从小到大的顺序排列为_____.
-
科目: 来源: 题型:
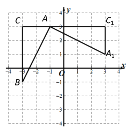
查看答案和解析>>【题目】如图,在平面直角坐标系中,有一Rt△ABC,∠C=90°且A(-1,3)、B(-3,-1)、C(-3,3),已知△A1AC1是由△ABC旋转得到的.若点Q在x轴上,点P在直线AB上,要使以Q、P、A1、C1为顶点的四边形是平行四边形,满足条件的点Q的坐标为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场有一种游戏,规则是:在一只装有8个红球和若干个白球(每个球除颜色外都相同)的不透明的箱子中,随机摸出1个球,摸到红球就可获得一瓶饮料.工作人员统计了参加游戏的人数和获得饮料的人数(见下表).
(1)计算并完成表格;
参加游戏的人数
200
300
400
500
获得饮料的人数
39
63
82
99
获得饮料的频率
(2)估计获得饮料的概率;
(3)请你估计袋中白球的数量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(a,0)和B(0,b)满足
 ,分别过点A、B作x轴、y轴的垂线交于点C,如图,点P从原点出发,以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动.
,分别过点A、B作x轴、y轴的垂线交于点C,如图,点P从原点出发,以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动.(1)写出A、B、C三点的坐标;
(2)当点P移动了6秒时,描出此时P点的位置,并写出点P的位置坐标;
(3)连结(2)中B、P两点,将线段BP向下平移h个单位(h>0),得到B′P′,若B′P′将四边形OACB的周长分成相等的两部分,求h的值.

相关试题

