【题目】已知OC是∠AOB内部的一条射线,∠AOC=30°,OE是∠COB的平分线.


(1)如图1,当∠COE=40°时,求∠AOB的度数;
(2)当OE⊥OA时,请在图中画出射线OE,OB,并直接写出∠AOB的度数.
参考答案:
【答案】(1) 110°;(2)作图见解析, ∠AOB=150°.
【解析】试题分析:(1)由OE为角平分线,得到∠COB=2∠COE,由![]() 的度数求出∠COB的度数,再由∠AOB=∠AOC+∠COB即可求出∠AOB的度数;
的度数求出∠COB的度数,再由∠AOB=∠AOC+∠COB即可求出∠AOB的度数;
(2)作出相应的图形,如图所示,由OE垂直于OA,根据∠AOC度数求出∠EOC 的度数,同理可得出∠AOB的度数.
解:(1)∵OE是∠COB的平分线(已知),
∴∠COB=2∠COE(角平分线定义).
∵∠COE=40°,
∴∠COB=80°.
∵∠AOC=30°,
∴∠AOB=∠AOC+∠COB=110°.
(2)如右图:

∵∠AOC=30°,OE⊥OA,
∴∠COE=60°.
∵OE是∠COB的平分线,
∴∠COB=2∠COE=120°.
∵∠AOC=30°,
∴∠AOB=∠AOC+∠COB=30°+120°=150°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,直线
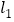 :
: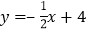 分别与x轴、y轴交于点A、点B,且与直线
分别与x轴、y轴交于点A、点B,且与直线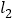 :
: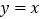 于点C.
于点C.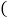 Ⅰ
Ⅰ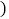 如图
如图 ,求出B、C两点的坐标;
,求出B、C两点的坐标;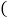 Ⅱ
Ⅱ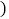 若D是线段OC上的点,且
若D是线段OC上的点,且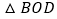 的面积为4,求直线BD的函数解析式.
的面积为4,求直线BD的函数解析式. Ⅲ
Ⅲ 如图
如图 ,在
,在 Ⅱ
Ⅱ 的条件下,设P是射线BD上的点,在平面内是否存在点Q,使以O、B、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
的条件下,设P是射线BD上的点,在平面内是否存在点Q,使以O、B、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.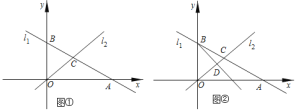
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.把△ABC绕AB边上的点D顺时针旋转90°得到△A′B′C′,A′C′交AB于点E.若AD=BE,则△A′DE的面积是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3.点D是BC边上的一动点(不与点B、C重合),过点D作DE⊥BC交AB于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处.当△AEF为直角三角形时,BD的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】5月31日是世界无烟日.某市卫生机构为了了解“导致吸烟人口比例高的最主要原因”,随机抽样调查了该市部分18﹣65岁的市民.如图是根据调查结果绘制的统计图,根据图中信息解答下列问题:

(1)这次接受随机抽样调查的市民总人数为;
(2)图1中的m的值是;
(3)求图2中认为“烟民戒烟的毅力弱”所对应的圆心角的度数;
(4)若该市18﹣65岁的市民约有200万人,请你估算其中认为导致吸烟人口比例高的最主要的原因是“对吸烟危害健康认识不足”的人数. -
科目: 来源: 题型:
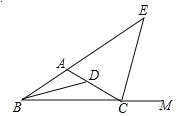
查看答案和解析>>【题目】如图所示,△ABC中,BD平分∠ABC,CE平分∠ACB的邻补角∠ACM,若∠BDC=130°,∠E=50°,则∠BAC的度数是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在所给图形中:
⑴求证:∠BDC=∠A+∠B+∠C;
⑵如果点D与点A分别在线段BC的两侧,猜想∠BDC、∠A、∠B、∠C这4个角之间有怎样的关系,并证明你的结论.

相关试题

