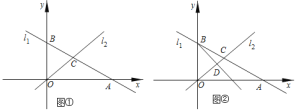
【题目】在平面直角坐标系中,直线![]() :
:![]() 分别与x轴、y轴交于点A、点B,且与直线
分别与x轴、y轴交于点A、点B,且与直线![]() :
:![]() 于点C.
于点C.
![]() Ⅰ
Ⅰ![]() 如图
如图![]() ,求出B、C两点的坐标;
,求出B、C两点的坐标;
![]() Ⅱ
Ⅱ![]() 若D是线段OC上的点,且
若D是线段OC上的点,且![]() 的面积为4,求直线BD的函数解析式.
的面积为4,求直线BD的函数解析式.
![]() Ⅲ
Ⅲ![]() 如图
如图![]() ,在
,在![]() Ⅱ
Ⅱ![]() 的条件下,设P是射线BD上的点,在平面内是否存在点Q,使以O、B、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
的条件下,设P是射线BD上的点,在平面内是否存在点Q,使以O、B、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
参考答案:
【答案】(Ⅰ)B(0,4)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ) Q的坐标为(2√2,-2√2)或(-2,2)或(4,4).
;(Ⅲ) Q的坐标为(2√2,-2√2)或(-2,2)或(4,4).
【解析】
(1) 令![]() ,得到
,得到![]() ,可求B坐标,解方程组可得得解得C的坐标;(2)由面积求出D的坐标,再由待定系数法求BD函数解析式;(3)
,可求B坐标,解方程组可得得解得C的坐标;(2)由面积求出D的坐标,再由待定系数法求BD函数解析式;(3)![]() 当OB为菱形的边时,
当OB为菱形的边时,![]() ,可得
,可得![]() ,
,![]() 当
当![]() 为菱形的对角线时,四边形
为菱形的对角线时,四边形![]() 是正方形,此时
是正方形,此时![]() .
.![]() 当OB为菱形的边时,点
当OB为菱形的边时,点![]() 与D重合,P、Q关于y轴对称,
与D重合,P、Q关于y轴对称,![]() .
.
解:![]() Ⅰ
Ⅰ![]() 对于直线:
对于直线:![]() ,令
,令![]() ,得到
,得到![]() ,
,![]() ,
,
由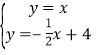 ,解得
,解得![]() ,
,
![]()
![]() Ⅱ
Ⅱ![]() 点D在直线
点D在直线![]() 上,设
上,设![]() ,
,![]() 的面积为4,
的面积为4,![]() ,
,
解得![]() ,
,![]() .
.
设直线BD的解析式为![]() ,则有
,则有![]() ,
,
解得![]() ,
,![]() 直线BD的解析式为
直线BD的解析式为![]() .
.![]() Ⅲ
Ⅲ![]() 如图
如图![]() 中,
中,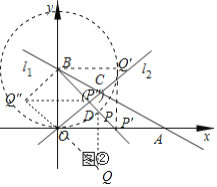
![]() 当OB为菱形的边时,
当OB为菱形的边时,![]() ,可得
,可得![]() ,
,![]()
![]() 当
当![]() 为菱形的对角线时,四边形
为菱形的对角线时,四边形![]() 是正方形,此时
是正方形,此时![]() .
.![]() 当OB为菱形的边时,点
当OB为菱形的边时,点![]() 与D重合,P、Q关于y轴对称,
与D重合,P、Q关于y轴对称,![]() ,
,
综上所述,满足条件的Q的坐标为![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,点E,F分别在边BC,AD上,且AF=CE.

(Ⅰ)如图①,求证四边形AECF是平行四边形;
(Ⅱ)如图②,若∠BAC=90°,且四边形AECF是边长为6的菱形,求BE的长.
-
科目: 来源: 题型:
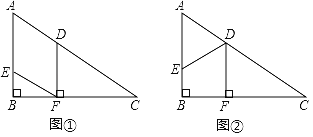
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,∠C=30°,AC=12cm,点E从点A出发沿AB以每秒lcm的速度向点B运动,同时点D从点C出发沿CA以每秒2cm的速度向点A运动,运动时间为t秒(0<t<6),过点D作DF⊥BC于点F.
(I)试用含t的式子表示AE、AD、DF的长;
(Ⅱ)如图①,连接EF,求证:四边形AEFD是平行四边形;
(Ⅲ)如图②,连接DE,当t为何值时,四边形EBFD是矩形?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B在反比例函数y=
 (k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M、N,延长线段AB交x轴于点C,若OM=MN=NC,△AOC的面积为6,则k的值为 .
(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M、N,延长线段AB交x轴于点C,若OM=MN=NC,△AOC的面积为6,则k的值为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.把△ABC绕AB边上的点D顺时针旋转90°得到△A′B′C′,A′C′交AB于点E.若AD=BE,则△A′DE的面积是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3.点D是BC边上的一动点(不与点B、C重合),过点D作DE⊥BC交AB于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处.当△AEF为直角三角形时,BD的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知OC是∠AOB内部的一条射线,∠AOC=30°,OE是∠COB的平分线.


(1)如图1,当∠COE=40°时,求∠AOB的度数;
(2)当OE⊥OA时,请在图中画出射线OE,OB,并直接写出∠AOB的度数.
相关试题

