Question

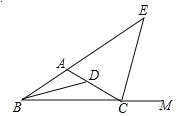
【题目】如图所示，△ABC中，BD平分∠ABC，CE平分∠ACB的邻补角∠ACM，若∠BDC=130°，∠E=50°，则∠BAC的度数是_______．

Answer 1

【答案】120°

【解析】

由三角形的一个外角等于与它不相邻的两个内角的和以及CE是外角的平分线列式求出∠B的度数，再根据BD为内角平分线求出∠ABD的度数，然后利用三角形的外角性质即可求出∠BAC的度数．

根据三角形的外角性质，∠DBC+∠BDC=2（∠ABC+∠E），
∵BD为内角平分线，
∴∠DBC=∠ABD，
∴∠ABC+130°=2（∠ABC+50°），
解得∠ABC=20°，
∴∠ABD=×20°=10°，
在△ABD中，∠BDC=∠ABD+∠BAC，
即130°=10°+∠BAC，
解得∠BAC=120°．
故答案为：120°．