【题目】已知关于![]() 的方程
的方程![]() .
.
![]() 求证:不论
求证:不论![]() 为任何实数,此方程总有实数根;
为任何实数,此方程总有实数根;
![]() 若方程
若方程![]() 有两个不同的整数根,且
有两个不同的整数根,且![]() 为正整数,求
为正整数,求![]() 的值.
的值.
参考答案:
【答案】(1)见解析;(2)m=1.
【解析】
(1)根据方程的系数结合根的判别式,即可得出△=(3m-1)2≥0,由此即可证出:不论m为任何实数,此方程总有实数根;
(2)利用分解因式法解一元二次方程,可得出方程的解,根据该方程有两个不等的整数根结合m为正整数,即可求出m的值.
(1)∵△=(3m+1)2-12m=9m2-6m+1=(3m-1)2.
∴不论m为任何实数时总有(3m-1)2≥0.
∴此时方程有实数根.
(2)∵mx2+(3m+1)x+3=0.
解得 x1=-3,x2=![]() .
.
∵方程mx2+(3m+1)x+3=0有两个不等的整数根,且m为正整数,
∴m=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点(1,3)在函数y=
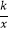 (x>0)的图象上,正方形ABCD的边BC在x轴上,点E是对角线AC、BD的交点,函数y=
(x>0)的图象上,正方形ABCD的边BC在x轴上,点E是对角线AC、BD的交点,函数y= 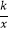 (x>0)的图象又经过A、E两点,则点E的坐标为 .
(x>0)的图象又经过A、E两点,则点E的坐标为 . 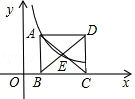
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:为了求1+3+32+33+…+3100的值,可设M=1+3+32+33+…+3100,则3M=3+32+33+34+…+3101,因此3M﹣M=3101﹣1.所以M=
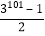 ,即1+3+32+33+…+3100=
,即1+3+32+33+…+3100=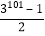 .问题解决:仿照上述方法求下列式子的值.
.问题解决:仿照上述方法求下列式子的值.(1)1+4+42+43+…+420.
(2)5101+5102+5103+…+52018.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一段抛物线y=﹣x(x﹣1)(0≤x≤1)记为m1 , 它与x轴交点为O、A1 , 顶点为P1;将m1绕点A1旋转180°得m2 , 交x轴于点A2 , 顶点为P2;将m2绕点A2旋转180°得m3 , 交x轴于点A3 , 顶点为P3 , …,如此进行下去,直至得m10 , 顶点为P10 , 则P10的坐标为

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC中,AB=AC=10厘米,BC=12厘米,D是BC的中点,点P从B出发,以a厘米/秒(a>0)的速度沿BA匀速向点A运动,点Q同时以1厘米/秒的速度从D出发,沿DB匀速向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,设它们运动的时间为t秒.

(1)若a=2,△BPQ∽△BDA,求t的值;
(2)设点M在AC上,四边形PQCM为平行四边形.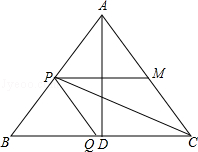
①若a= ,求PQ的长;
,求PQ的长;
②是否存在实数a,使得点P在∠ACB的平分线上?若存在,请求出a的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2﹣
 x﹣2(a≠)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
x﹣2(a≠)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).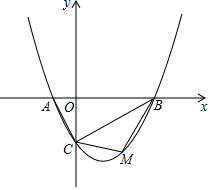
(1)求抛物线的解析式;
(2)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标;
(3)试探究:△ABC的外接圆的圆心位置,并求出圆心坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】为鼓励居民节约用水,某市对居民用水收费实行“阶梯水价”,按每年用水量统计,不超过180立方米的部分按每立方米5元收费;超过180立方米不超过260立方米的部分按每立方米7元收费;超过260立方米的部分按每立方米9元收费.
(1)设每年用水量为x立方米,按“阶梯水价”应缴水费y元,请写出y(元)与x(立方米)之间的函数解析式;
(2)明明家预计2015年全年用水量为200立方米,那么按“阶梯水价”收费,她家应缴水费多少元?
相关试题

