【题目】某人用如下方法测一钢管的内径:将一小段钢管竖直放在平台上.向内放入两个半径为5 cm的钢球,测得上面一个钢球的最高点到底面的距离DC=16 cm(钢管的轴截面如图所示),则钢管的内径AD的长为_______cm.

参考答案:
【答案】18
【解析】试题解析:如图,连接OO′,作OF⊥DC于F,OE⊥AD于E,O′G⊥AB于G,O′H⊥BC于H,O′M⊥DC于M.
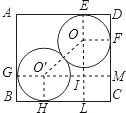
根据题意得出:正方形BHO′G和正方形EOFD,
∴BG=DE=球的半径,然后可得出GM∥BC,EL∥DC,
![]() 直角三角形的斜边是OO′=10,
直角三角形的斜边是OO′=10,
其中一条直角边OI=ELEOIL=DCEOO′H=1610=6,
则根据勾股定理得另一条直角边O′I=8.
则钢管的直径GM=GO′+O′I+IM=8+5+5=18.
故答案为:18.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,在三角形ABC中,
,在三角形ABC中, ,点D为边BC的中点,射线
,点D为边BC的中点,射线 交AB于点
交AB于点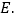 点P从点D出发,沿射线DE以每秒1个单位长度的速度运动
点P从点D出发,沿射线DE以每秒1个单位长度的速度运动 以PD为斜边,在射线DE的右侧作等腰直角
以PD为斜边,在射线DE的右侧作等腰直角 设点P的运动时间为
设点P的运动时间为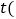 秒
秒 .
.
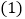 用含t的代数式表示线段EP的长.
用含t的代数式表示线段EP的长. 求点Q落在边AC上时t的值.
求点Q落在边AC上时t的值. 当点Q在
当点Q在 内部时,设
内部时,设 和
和 重叠部分图形的面积为
重叠部分图形的面积为 平方单位
平方单位 ,求S与t之间的函数关系式.
,求S与t之间的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,点E为AD上一点,FG⊥CE分别交AB、CD于F、G,垂足为O.
(1)求证:CE=FG;
(2)如图2,连接OB,若AD=3DE,∠OBC=2∠DCE。
求
 的值;
的值;若AD=3,则OE的长为_________(直接写出结果).


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为6,B是数轴上在A左侧的一点,且A,B两点间的距离为10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)数轴上点B表示的数是 ,点P表示的数是 (用含t的代数式表示);
(2)动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发.求:
①当点P运动多少秒时,点P与点Q相遇?
②当点P运动多少秒时,点P与点Q间的距离为8个单位长度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料并解决有关问题:我们知道
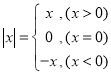 ,所以当
,所以当 时,
时,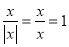 ;当
;当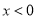 时,
时, ,现在我们可以用这个结论来解决下面问题:
,现在我们可以用这个结论来解决下面问题:(1)已知
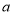 ,
,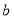 是有理数,当
是有理数,当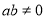 时,求
时,求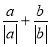 的值;
的值;(2)已知
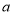 ,
,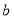 ,
,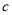 是有理数,当
是有理数,当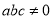 ,求
,求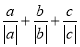 的值;
的值;(3)已知
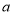 ,
,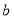 ,
,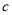 是有理数,
是有理数,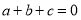 ,
,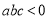 ,求
,求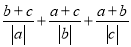 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的大括号中:8,﹣
 ,+2.8,π,
,+2.8,π,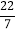 ,﹣0.003,0,﹣100,﹣3.626626662……
,﹣0.003,0,﹣100,﹣3.626626662……正数集合{_____ …}
整数集合{_____…}
负分数集合{_____ …}
无理数集合{_____ …}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 1,直线 y=﹣
 x+6 与 y 轴于点 A,与 x 轴交于点 D,直线 AB 交 x 轴于点 B,
x+6 与 y 轴于点 A,与 x 轴交于点 D,直线 AB 交 x 轴于点 B, AOB 沿直线 AB 折叠,点 O 恰好落在直线 AD 上的点 C 处.
AOB 沿直线 AB 折叠,点 O 恰好落在直线 AD 上的点 C 处.(1)求点 B 的坐标;

(2)如图 2,直线 AB 上的两点 F、G,
 DFG 是以 FG 为斜边的等腰直角三角形,求点 G 的坐标;
DFG 是以 FG 为斜边的等腰直角三角形,求点 G 的坐标;
(3)如图 3,点 P 是直线 AB 上一点,点 Q 是直线 AD 上一点,且 P、Q 均在第四象限,点 E 是 x 轴上一点,若四边形 PQDE 为菱形,求点 E 的坐标.

相关试题

