【题目】如图![]() ,在三角形ABC中,
,在三角形ABC中,![]() ,点D为边BC的中点,射线
,点D为边BC的中点,射线![]() 交AB于点
交AB于点![]() 点P从点D出发,沿射线DE以每秒1个单位长度的速度运动
点P从点D出发,沿射线DE以每秒1个单位长度的速度运动![]() 以PD为斜边,在射线DE的右侧作等腰直角
以PD为斜边,在射线DE的右侧作等腰直角![]() 设点P的运动时间为
设点P的运动时间为![]() 秒
秒![]() .
.

![]() 用含t的代数式表示线段EP的长.
用含t的代数式表示线段EP的长.
![]() 求点Q落在边AC上时t的值.
求点Q落在边AC上时t的值.
![]() 当点Q在
当点Q在![]() 内部时,设
内部时,设![]() 和
和![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() 平方单位
平方单位![]() ,求S与t之间的函数关系式.
,求S与t之间的函数关系式.
参考答案:
【答案】(1)点P在线段DE上时,EP=3-t,当点P在DE延长线上时,PE=t-3;(2)t=8;(3)
【解析】试题分析:(1)分点P在线段DE上和在DE的延长线上两种情况讨论即可得;
(2)如图所示,当点Q落在边AC上时,过点Q作![]() 于F,由题意可得FQ=CD=4,再根据等腰直角三角形可得PD=2FQ,从而可得;
于F,由题意可得FQ=CD=4,再根据等腰直角三角形可得PD=2FQ,从而可得;
(3)分点P在线段DE上和在DE的延长线上两种情况讨论即可得.
试题解析:![]() 由题可得,
由题可得,![]() ,
,
当点P在线段DE上时,![]() ;
;
当点P在DE的延长线上时,![]() ;
;
![]() 如图所示,当点Q落在边AC上时,过点Q作
如图所示,当点Q落在边AC上时,过点Q作![]() 于F,
于F,

![]() ,
,
![]() 四边形CDFQ是矩形,
四边形CDFQ是矩形,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
![]() ;
;
![]() 当点P在线段DE上时,
当点P在线段DE上时,![]() 和
和![]() 重叠部分为
重叠部分为![]() ,且
,且![]() 边上的高为
边上的高为![]() ,
,

![]() 点P从点D运动到点E处时,时间为3s,
点P从点D运动到点E处时,时间为3s,
![]() 当
当![]() 时,
时,![]() ,
,
![]() 当点P在线段DE的延长线上时,
当点P在线段DE的延长线上时,![]() 和
和![]() 重叠部分为四边形EDQG,
重叠部分为四边形EDQG,
如图所示,过G作![]() 于F,则
于F,则![]() ∽
∽![]() ,且
,且![]() ,
,

![]() ,
,
![]() :
:![]() :
:![]() :
:![]() :4,
:4,
![]() ,
,
![]() ,
,
![]() 的面积
的面积![]() ,
,
由![]() 可知,点Q落在边AC上时,t的值为8s,
可知,点Q落在边AC上时,t的值为8s,
![]() 当
当![]() 时,
时,![]() ,
,
综上所述,S与t之间的函数关系式为: .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)
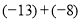
(2)
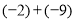
(3)
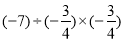
(4)
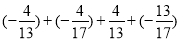
(5)
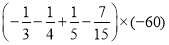
(6)
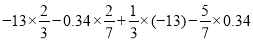
(7)

(8)
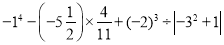
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个点从数轴上的原点开始,先向右移动了3个单位长度,再向左移动 5 个单位长度,可以看到终点表示的数是
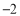 .已知点
.已知点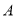 、
、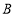 是数轴上的点,完成下列各题:
是数轴上的点,完成下列各题: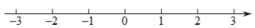
(1)如果点
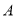 表示数- 3,将点
表示数- 3,将点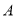 向右移动 7 个单位长度,那么终点
向右移动 7 个单位长度,那么终点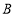 表示的数是 ,
表示的数是 ,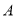 、
、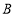 两点间的距离是 .
两点间的距离是 .(2)如果点
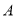 表示数是3,将点
表示数是3,将点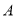 向左移动 7 个单位长度,再向右移动5 个单位长度,那么终点
向左移动 7 个单位长度,再向右移动5 个单位长度,那么终点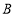 表示的数是 ,
表示的数是 ,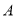 、
、 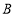 两点间的距离是 .
两点间的距离是 .(3)一般地,如果点
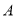 表示数为
表示数为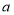 ,将点
,将点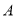 向右移动
向右移动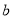 个单位长度,再向左移动
个单位长度,再向左移动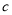 个单位长度,那么请你猜想终点
个单位长度,那么请你猜想终点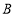 表示的数是 ,
表示的数是 ,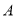 、
、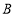 两点间的距离是 .
两点间的距离是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】(2014河南21题)某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍.设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下降
 元,且限定商店最多购进A型电脑70台.若商店保持两种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
元,且限定商店最多购进A型电脑70台.若商店保持两种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,点E为AD上一点,FG⊥CE分别交AB、CD于F、G,垂足为O.
(1)求证:CE=FG;
(2)如图2,连接OB,若AD=3DE,∠OBC=2∠DCE。
求
 的值;
的值;若AD=3,则OE的长为_________(直接写出结果).


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为6,B是数轴上在A左侧的一点,且A,B两点间的距离为10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)数轴上点B表示的数是 ,点P表示的数是 (用含t的代数式表示);
(2)动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发.求:
①当点P运动多少秒时,点P与点Q相遇?
②当点P运动多少秒时,点P与点Q间的距离为8个单位长度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某人用如下方法测一钢管的内径:将一小段钢管竖直放在平台上.向内放入两个半径为5 cm的钢球,测得上面一个钢球的最高点到底面的距离DC=16 cm(钢管的轴截面如图所示),则钢管的内径AD的长为_______cm.

相关试题

