搜索
【题目】把下列各数填在相应的大括号中：8，﹣
，+2.8，π，
，﹣0.003，0，﹣100，﹣3.626626662……
正数集合{_____ …}
整数集合{_____…}
负分数集合{_____ …}
无理数集合{_____ …}．
参考答案：
【答案】8，+2.8，π，
8，0，﹣100 ﹣
，﹣0.003 π，﹣3.626626662……
【解析】
利用实数的概念及分类进行解答。
解：正数集合{ 8，+2.8，π，，…}
整数集合{8，0，﹣100…}
负分数集合{﹣，﹣0.003 …}
无理数集合{π，﹣3.626626662………}．
故答案为：(1)8，+2.8，π，；(2)8，0，﹣100；(3)﹣，﹣0.003；(4)π，﹣3.626626662……
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在等腰直角△ABC中，∠BAC=90°，AB=AC=2，点E是BC边上一点，∠DEF=45°且角的两边分别与边AB，射线CA交于点P，Q．
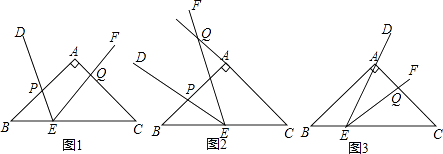
（1）如图2，若点E为BC中点，将∠DEF绕着点E逆时针旋转，DE与边AB交于点P，EF与CA的延长线交于点Q．设BP为x，CQ为y，试求y与x的函数关系式，并写出自变量x的取值范围；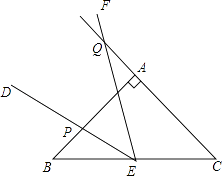
（2）如图3，点E在边BC上沿B到C的方向运动（不与B，C重合），且DE始终经过点A，EF与边AC交于Q点．探究：在∠DEF运动过程中，△AEQ能否构成等腰三角形，若能，求出BE的长；若不能，请说明理由．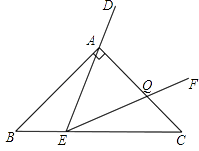
-
科目： 来源： 题型：
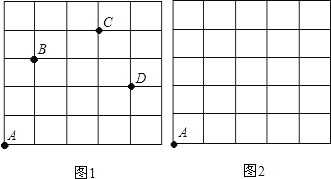
查看答案和解析>>【题目】如图，一只甲虫在5
5的方格（每一格边长为1）上沿着网格线运动,从A处出发去看望B、C、D处的甲虫，规定：向上向右为正，向下向左为负.例如：从A到B记为：
（+1，+3）；从C到D 记为: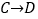
（+1，-2）,其中第一个数表示左右方向，第二个数表示上下方向.(1)填空：
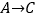记为（ ， ）, 
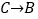记为（ ， ）；(2)若甲虫的行走路线为：
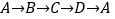,请你计算甲虫走过的路程.(3)若这只甲虫去Q的行走路线依次为：A→M（+2，+2），M→N（+2，-1），N→P（-2，+3），P→Q（-1，-2），请依次在图2标出点M、N、P、Q的位置．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，D是BC的中点，过D点的直线GF交AC于F，交AC的平行线BG于G点，DE⊥DF，交AB于点E，连结EG、EF．
（1）求证：BG＝CF．
（2）请你判断BE+CF与EF的大小关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，⊙C的半径为r，P是与圆心C不重合的点，点P关于⊙C的限距点的定义如下：若P′为直线PC与⊙C的一个交点，满足r≤PP′≤2r，则称P′为点P关于⊙C的限距点，如图为点P及其关于⊙C的限距点P′的示意图．
（1）当⊙O的半径为1时．
①分别判断点M（3，4），N（
，0），T（1， 
）关于⊙O的限距点是否存在？若存在，求其坐标；
②点D的坐标为（2，0），DE，DF分别切⊙O于点E，点F，点P在△DEF的边上．若点P关于⊙O的限距点P′存在，求点P′的横坐标的取值范围；
（2）保持（1）中D，E，F三点不变，点P在△DEF的边上沿E→F→D→E的方向运动，⊙C的圆心C的坐标为（1，0），半径为r，请从下面两个问题中任选一个作答．问题1
问题2
若点P关于⊙C的限距点P′存在，且P′随点P的运动所形成的路径长为πr，则r的最小值为
．若点P关于⊙C的限距点P′不存在，则r的取值范围为
． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知等边△ABC的边长为4cm，点P，Q分别从B，C两点同时出发，其中点P沿BC向终点C运动，速度为1cm/s；
点Q沿CA，AB向终点B运动，速度为2cm/s，设它们运动的时间为x（s），
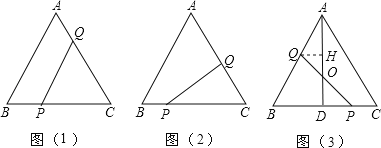
（1）如图（1），当x为何值时，PQ∥AB；
（2）如图（2），若PQ⊥AC，求x；
（3）如图（3），当点Q在AB上运动时，PQ与△ABC的高AD交于点O，OQ与OP是否总是相等？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知动点P在函数
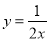（x＞0）的图象上运动，PM⊥x轴于点M，PN⊥y轴于点N，线段PM、PN分别与直线AB：y=﹣x+1交于点E，F，则AFBE的值为（ ）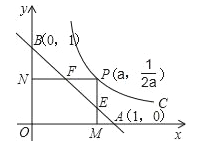
A. 4 B. 2 C. 1 D.
相关试题
