【题目】如图 1,直线 y=﹣![]() x+6 与 y 轴于点 A,与 x 轴交于点 D,直线 AB 交 x 轴于点 B,
x+6 与 y 轴于点 A,与 x 轴交于点 D,直线 AB 交 x 轴于点 B,![]() AOB 沿直线 AB 折叠,点 O 恰好落在直线 AD 上的点 C 处.
AOB 沿直线 AB 折叠,点 O 恰好落在直线 AD 上的点 C 处.
(1)求点 B 的坐标;

(2)如图 2,直线 AB 上的两点 F、G,![]() DFG 是以 FG 为斜边的等腰直角三角形,求点 G 的坐标;
DFG 是以 FG 为斜边的等腰直角三角形,求点 G 的坐标;

(3)如图 3,点 P 是直线 AB 上一点,点 Q 是直线 AD 上一点,且 P、Q 均在第四象限,点 E 是 x 轴上一点,若四边形 PQDE 为菱形,求点 E 的坐标.

参考答案:
【答案】(1)B的坐标为(3,0);(2)G的坐标为(2,2);(3)E的坐标为(﹣2,0).
【解析】
(1)设BC=OB=x,则BD=8﹣x,在Rt![]() BCD中,根据BC2+CD2=BD2,构建方程即可解决问题;
BCD中,根据BC2+CD2=BD2,构建方程即可解决问题;
(2)作GM⊥x轴于M,FN⊥x轴于N,由![]() DMG≌
DMG≌![]() FND(AAS),推出GM=DN,DM=FN,设GM=DM=m,DM=FN=n,根据G、F在直线AB上,构建方程组即可解决问题;
FND(AAS),推出GM=DN,DM=FN,设GM=DM=m,DM=FN=n,根据G、F在直线AB上,构建方程组即可解决问题;
(3)如图,设Q(a,﹣![]() a+6),因为PQ∥x轴,且点P在直线y=﹣2x+6上,推出P(
a+6),因为PQ∥x轴,且点P在直线y=﹣2x+6上,推出P(![]() a,﹣
a,﹣![]() a+6),PQ=
a+6),PQ=![]() a,作QH⊥x轴于H.由勾股定理可知:QH:DH:DQ=3:4:5,想办法构建方程即可解决问题.
a,作QH⊥x轴于H.由勾股定理可知:QH:DH:DQ=3:4:5,想办法构建方程即可解决问题.
解:(1)对于直线y=﹣![]() x+6,
x+6,
令x=0,得到y=6,可得A(0,6),
令y=0,得到x=8,可得D(8,0),
∴AC=AO=6,OD=8,AD=![]() =10,
=10,
∴CD=AD﹣AC=4,设BC=OB=x,则BD=8﹣x,
在Rt![]() BCD中,∵BC2+CD2=BD2,
BCD中,∵BC2+CD2=BD2,
∴x2+42=(8﹣x)2,
∴x=3,
∴B(3,0).
(2)设直线AB的解析式为y=kx+6,
∵B(3,0),
∴3k+6=0,
∴k=﹣2,
∴直线AB的解析式为y=﹣2x+6,
作GM⊥x轴于M,FN⊥x轴于N,

∵![]() DFG是等腰直角三角形,
DFG是等腰直角三角形,
∴DG=FD,∠1=∠2,∠DMG=∠FND=90°,
∴![]() DMG≌
DMG≌![]() FND(AAS),
FND(AAS),
∴GM=DN,DM=FN,
设GM=DN=m,DM=FN=n,
∵G、F在直线AB上,
则:m=﹣2(8﹣n)+6,﹣n=﹣2(8﹣m)+6,
解得:m=2,n=6
∴OM=OD﹣DM=2,GM=2,
∴G(2,2).
(3)①当点E在y轴左侧时,
如图,设Q(a,﹣![]() a+6),
a+6),
∵PQ∥x轴,且点P在直线y=﹣2x+6上,
∴P(![]() a,﹣
a,﹣![]() a+6),
a+6),
∴PQ=![]() a,作QH⊥x轴于H.
a,作QH⊥x轴于H.

∴DH=a﹣8,QH=![]() a﹣6,
a﹣6,
∴![]() =
=![]() ,
,
由勾股定理可知:QH:DH:DQ=3:4:5,
∴QH=![]() DQ=
DQ=![]() a,
a,
∴![]() a=
a=![]() a﹣6,
a﹣6,
∴a=16,
∴Q(16,﹣6),P(6,﹣6),
∵ED∥PQ,ED=PQ,D(8,0),
∴E(﹣2,0).
②当点E在y轴右侧时,
同理可得:点E(3.4,0)(舍去);
故点E的坐标为(﹣2,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某人用如下方法测一钢管的内径:将一小段钢管竖直放在平台上.向内放入两个半径为5 cm的钢球,测得上面一个钢球的最高点到底面的距离DC=16 cm(钢管的轴截面如图所示),则钢管的内径AD的长为_______cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料并解决有关问题:我们知道
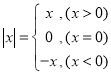 ,所以当
,所以当 时,
时,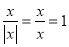 ;当
;当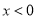 时,
时, ,现在我们可以用这个结论来解决下面问题:
,现在我们可以用这个结论来解决下面问题:(1)已知
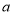 ,
,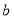 是有理数,当
是有理数,当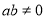 时,求
时,求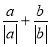 的值;
的值;(2)已知
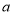 ,
,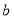 ,
,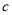 是有理数,当
是有理数,当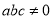 ,求
,求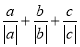 的值;
的值;(3)已知
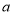 ,
,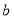 ,
,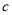 是有理数,
是有理数,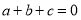 ,
,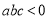 ,求
,求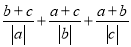 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的大括号中:8,﹣
 ,+2.8,π,
,+2.8,π,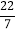 ,﹣0.003,0,﹣100,﹣3.626626662……
,﹣0.003,0,﹣100,﹣3.626626662……正数集合{_____ …}
整数集合{_____…}
负分数集合{_____ …}
无理数集合{_____ …}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某摩托车厂本周计划每日生产450辆摩托车,由于工人实行轮休, 每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表: [增加的辆数为正数,减少的辆数为负数]
星期
一
二
三
四
五
六
日
增减
-5
+7
-3
+4
+10
-9
-25
(1)本周星期六生产多少辆摩托车?
(2)本周总产量与计划产量相比,是增加了还是减少了?为什么?
(3)产量最多的那天比产量最少的那天多生产多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是半圆O的直径,点C是半圆O上的动点,点D是线段AB延长线上的动点,在运动过程中,保持CD=OA.
(1)当直线CD与半圆O相切时(如图①),求∠ODC的度数;
(2)当直线CD与半圆O相交时(如图②),设另一交点为E,连接AE,若AE∥OC,
①AE与OD的大小有什么关系?为什么?
②求∠ODC的度数.
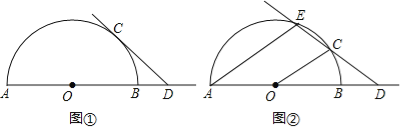
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,函数y=ax+b与y=ax2-bx的图象可能是( )
A.
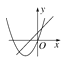 B.
B. 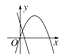 C.
C. 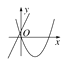 D.
D. 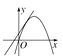
相关试题

