【题目】如图,已知数轴上点A表示的数为6,B是数轴上在A左侧的一点,且A,B两点间的距离为10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)数轴上点B表示的数是 ,点P表示的数是 (用含t的代数式表示);
(2)动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发.求:
①当点P运动多少秒时,点P与点Q相遇?
②当点P运动多少秒时,点P与点Q间的距离为8个单位长度?
![]()
参考答案:
【答案】(1)-4 ,6-6t ;(2)①点P运动5秒时;②点P运动1或9秒时.
【解析】
(1)由已知得OA=6,则OB=AB-OA=4,因为点B在原点左边,从而写出数轴上点B所表示的数;动点P从点A出发,运动时间为t(t>0)秒,所以运动的单位长度为6t,因为沿数轴向左匀速运动,所以点P所表示的数是6-6t;
(2)①点P运动t秒时追上点Q,由于点P要多运动10个单位才能追上点Q,则6t=10+4t,然后解方程得到t=5;
②分两种情况:当点P运动a秒时,不超过Q,则10+4t-6t=8;超过Q,则10+4t+8=6t;由此求得答案解即可.
解:(1)-4 ,6-6t ;
(2)①根据题意,得6t=10+4t,解得t=5.
答:当点P运动5秒时,点P与点Q相遇.
②当点P在点Q右边时,10+4t-6t=8,解得t=1;
当点P在点Q左边时,10+4t+8=6t,解得t=9.
答:当点P运动1或9秒时,点P与点Q间的距离为8个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程中解为x=3的方程是( )
A. 3x+1=5x-5 B. 2(x+3)=-x+9
C. 3(1-2x)-2(x+3)=0 D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD,DE∥AC.
(1)求证:四边形 OCED 为菱形
(2)若AD=7,AB=4,求四边形 OCED的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】老师在黑板上出了一道解方程的题:
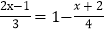 ,小明马上举起了手,要求到黑板上去做,他是这样做的:
,小明马上举起了手,要求到黑板上去做,他是这样做的:去分母,得4(2x-1)=1-3(x+2). ①
去括号,得8x-4=1-3x-6. ②
移项,得8x+3x=l-6+4 . ③
合并同类项,得11x=-1. ④
系数化为1,得x=-
 . ⑤
. ⑤老师说:小明解一元一次方程的一般步骤都掌握了,但解题时有一步做错了,他错在第 步(填编号),请你将正确的解方程过程写出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②a﹣b+c<0,③2a=b,④4a+2b+c>0,⑤若点(﹣2,y1)和(﹣
 ,y2)在该图象上,则y1>y2 . 其中正确的结论是(填入正确结论的序号).
,y2)在该图象上,则y1>y2 . 其中正确的结论是(填入正确结论的序号). 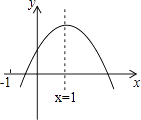
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF.
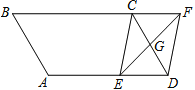
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;②当AE= cm时,四边形CEDF是菱形.(直接写出答案,不需要说明理由)
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数中y=ax2+bx﹣3的x、y满足表:
x
…
﹣1
0
1
2
3
…
y
…
0
﹣3
﹣4
﹣3
m
…
(1)求该二次函数的解析式;
(2)求m的值并直接写出对称轴及顶点坐标.
相关试题

