【题目】如图,抛物线的对称轴是直线x=2,顶点A的纵坐标为1,点B(4,0)在此抛物线上.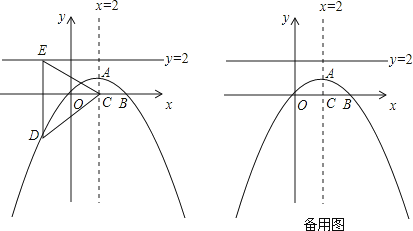
(1)求此抛物线的解析式;
(2)若此抛物线对称轴与x轴交点为C,点D(x,y)为抛物线上一动点,过点D作直线y=2的垂线,垂足为E.
①用含y的代数式表示CD2 , 并猜想CD2与DE2之间的数量关系,请给出证明;
②在此抛物线上是否存在点D,使∠EDC=120°?如果存在,请直接写出D点坐标;如果不存在,请说明理由.
参考答案:
【答案】
(1)
解:依题意,设抛物线的解析式为:y=a(x﹣2)2+1,代入B(4,0),得:
a(4﹣2)2+1=0,解得:a=﹣ ![]()
∴抛物线的解析式:y=﹣ ![]() (x﹣2)2+1
(x﹣2)2+1
(2)
解:
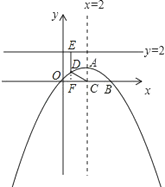
①猜想:CD2=DE2;
证明:由D(x,y)、C(2,0)、E(x,2)知:
CD2=(x﹣2)2+y2,DE2=(y﹣2)2;
由(1)知:(x﹣2)2=﹣4(y﹣1)=﹣4y+4,代入CD2中,得:
CD2=y2﹣4y+4=(y﹣2)2=DE2.
②由于∠EDC=120°>90°,所以点D必在x轴上方,且抛物线对称轴左右两侧各有一个,以左侧为例:
延长ED交x轴于F,则EF⊥x轴;
在Rt△CDF中,∠FDC=180°﹣120°=60°,∠DCF=30°,则:
CD=2DF、CF= ![]() DF;
DF;
设DF=m,则:CF= ![]() m、CD=DE=2m;
m、CD=DE=2m;
∵EF=ED+DF=2m+m=2,
∴m= ![]() ,DF=m=
,DF=m= ![]() ,CF=
,CF= ![]() m=
m= ![]() ,OF=OC﹣CF=2﹣
,OF=OC﹣CF=2﹣ ![]() ,
,
∴D(2﹣ ![]() ,
, ![]() );
);
同理,抛物线对称轴右侧有:D(2+ ![]() ,
, ![]() );
);
综上,存在符合条件的D点,且坐标为(2﹣ ![]() ,
, ![]() )或(2+
)或(2+ ![]() ,
, ![]() ).
).
【解析】(1)已知抛物线的顶点坐标,可以将抛物线的解析式设为顶点式,再代入B点的坐标求解即可.(2)①由坐标系两点间的距离公式不难得到CD2和DE2的表达式,再将(1)的抛物线解析式代入CD2的表达式中,用y替换掉x后,比较两者的大小关系即可;②∠EDC是钝角,那么点D一定在x轴的上方,且抛物线对称轴的左右两侧各一个(它们关于抛物线对称轴对称),延长ED交x轴于F,在Rt△CDF中,∠DCF=30°,那么DC=2DF、CF= ![]() DF,设出DF的长后,可以表示出CD、DE的长,由EF=ED+DF=2即可得出DF的长,从而求出点D的坐标.
DF,设出DF的长后,可以表示出CD、DE的长,由EF=ED+DF=2即可得出DF的长,从而求出点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在数轴上
 点表示数
点表示数 ,
, 点表示数
点表示数 ,且
,且 、
、 满足
满足

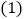 点
点 表示的数为________;点
表示的数为________;点 表示的数为________.
表示的数为________. 若点
若点 与点
与点 之间的距离表示为
之间的距离表示为 ,点
,点 与点
与点 之间的距离表示为
之间的距离表示为 ,请在数轴上找一点
,请在数轴上找一点 ,使
,使 ,则
,则 点表示的数________.
点表示的数________. 若在原点
若在原点 处放一挡板,一小球甲从点
处放一挡板,一小球甲从点 处以
处以 个单位/秒的速度向左运动;同时另一小球乙从点
个单位/秒的速度向左运动;同时另一小球乙从点 处以
处以 个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为
个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为 (秒),请分别表示出甲、乙两小球到原点的距离(用含
(秒),请分别表示出甲、乙两小球到原点的距离(用含 的代数式表示).
的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形OABC中,点B的坐标是(4,4),点E、F分别在边BC、BA上,OE=2
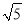 ,若∠EOF=45°,则F点的纵坐标是( )
,若∠EOF=45°,则F点的纵坐标是( )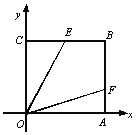
A.
 B. 1 C.
B. 1 C. 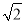 D.
D. 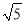 -1
-1 -
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连结菱形各边中点得到的四边形是____________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义新运算;对于任意有理数
 ,
, ,都有
,都有 ,等式右边是通常的加法、减法及乘法运算,比如,数字
,等式右边是通常的加法、减法及乘法运算,比如,数字 和
和 在该新运算下结果为
在该新运算下结果为 ,计算如下:
,计算如下:
 求
求 的值;
的值; 任意有理数
任意有理数 ,
, 请你重新定义一种新运算“
请你重新定义一种新运算“ ”,使得数字
”,使得数字 和
和 在你定义的新运算下运算的结果为
在你定义的新运算下运算的结果为 ;写出你定义的新运算________.
;写出你定义的新运算________. -
科目: 来源: 题型:
查看答案和解析>>【题目】福鼎市南溪水库的警戒水位是
 ,以下是南溪水库管理处七月份某周监测到的水位变化情况,上周末恰好达到警戒水位(正数表示比前一天水位高,负数表示比前一天水位低).
,以下是南溪水库管理处七月份某周监测到的水位变化情况,上周末恰好达到警戒水位(正数表示比前一天水位高,负数表示比前一天水位低).星期
一
二
三
四
五
六
日
水位变化









 星期四的水位是多少?
星期四的水位是多少? 从这周一到周日哪天的水位是最高的?
从这周一到周日哪天的水位是最高的? 以警戒水位为零点,用折线图表表示本周水位情况.
以警戒水位为零点,用折线图表表示本周水位情况. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的周长为24cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长等于( )

A.3cm
B.4cm
C.2.5cm
D.2cm
相关试题

