搜索
【题目】如图，在□ABCD中，∠ADC的平分线交AB于点E，∠ABC的平分线交CD于点F，求证：四边形EBFD是平行四边形．
参考答案：
【答案】见解析
【解析】试题分析：由在ABCD中，∠ABC的平分线交CD于点F，∠ADC的平分线交AB于点E，易证得∠ADE=∠CBF，从而得到△ADE≌△CBF，继而证得DF=EB，由DF∥BE，则可证得四边形EBFD是平行四边形．
试题解析：证明：∵四边形ABCD是平行四边形，∴AD=CB，∠A=∠C，∠ADC=∠ABC．
又∵∠ADE=
∠ADC，∠CBF=
∠ABC，∴∠ADE=∠CBF，∴△ADE≌△CBF，∴AE=CF，∴AB﹣AE=CD﹣CF，即DF=EB．又∵DF∥EB，∴四边形EBFD是平行四边形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知钝角三角形ABC，将△ABC绕点A按逆时针方向旋转110°得到△AB′C′，连接BB′，若AC′∥BB′，则∠CAB′的度数为（ ）
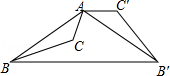
A.55°
B.65°
C.75°
D.85° -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将斜边长为4，∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B，弧
、 
是旋转过程中A、C的运动轨迹，则图中阴影部分的面积为（ ）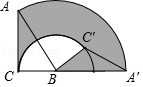
A.4π+2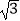
B.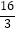
π﹣2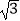
C.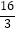
π+2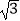
D.4π -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为﹣1，3，则下列结论正确的个数有（ ） ①ac＜0；②2a+b=0；③4a+2b+c＞0；④对于任意x均有ax2+bx≥a+b．
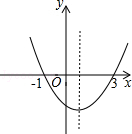
A.1
B.2
C.3
D.4 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图∠1=∠2，CF⊥AB，DE⊥AB，求证：FG∥BC.
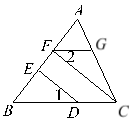
证明：∵CF⊥AB，DE⊥AB （已知）
∴∠BED=90°，∠BFC=90°（ ）
∴∠BED=∠BFC （ ）
∴ED∥FC （ ）
∴∠1=∠BCF （ ）
∵∠2=∠1 （ 已知 ）
∴∠2=∠BCF （ ）
∴FG∥BC （ ）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，E是△ABC中BC边上的一点，且BE=
BC；点D是AC上一点，且AD= 
AC，S△ABC=24，则S△BEF﹣S△ADF=（ ）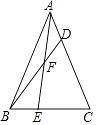 
A.1
B.2
C.3
D.4 -
科目： 来源： 题型：
查看答案和解析>>【题目】小刚在课外书中看到这样一道有理数的混合运算题：
计算：
她发现，这个算式反映的是前后两部分的和，而这两部分之间存在着某种关系，利用这种关系，他顺利地解答了这道题。
（1）前后两部分之间存在着什么关系？
（2）先计算哪步分比较简便？并请计算比较简便的那部分。
（3）利用（1）中的关系，直接写出另一部分的结果。
（4）根据以上分析，求出原式的结果。
相关试题
