【题目】如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( ) 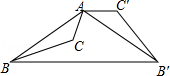
A.55°
B.65°
C.75°
D.85°
参考答案:
【答案】C
【解析】解:∵将△ABC绕点A按逆时针方向旋转l10°得到△AB′C′, ∴∠BAB′=∠CAC′=110°,AB=AB′,
∴∠AB′B= ![]() (180°﹣110°)=35°,
(180°﹣110°)=35°,
∵AC′∥BB′,
∴∠C′AB′=∠AB′B=35°,
∴∠CAB′=∠CAC′﹣∠C′AB′=110°﹣35°=75°.
故选C.
先根据旋转的性质得到∠BAB′=∠CAC′=110°,AB=AB′,根据等腰三角形的性质易得∠AB′B=35°,再根据平行线的性质得出∠C′AB′=∠AB′B=35°,然后利用∠CAB′=∠CAC′﹣∠C′AB′进行计算即可得出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2﹣2bx﹣3(b为常数,b<0).
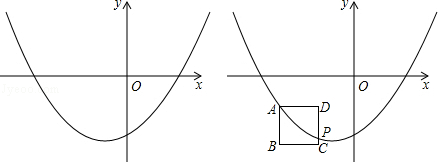
(1)抛物线y=x2﹣2bx﹣3总经过一定点,定点坐标为;
(2)抛物线的对称轴为直线x=(用含b的代数式表示),位于y轴的
侧.
(3)思考:若点P(﹣2,﹣1)在抛物线y=x2﹣2bx﹣3上,抛物线与反比例函数y=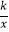 (k>0,x>0)的图象在第一象限内交点的横坐标为a,且满足2<a<3,试确定k的取值范围.
(k>0,x>0)的图象在第一象限内交点的横坐标为a,且满足2<a<3,试确定k的取值范围.
(4)探究:设点A是抛物线上一点,且点A的横坐标为m,以点A为顶点做边长为1的正方形ABCD,AB⊥x轴,点C在点A的右下方,若抛物线与CD边相交于点P(不与D点重合且不在y轴上),点P的纵坐标为﹣3,求b与m之间的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的正弦值等于( )
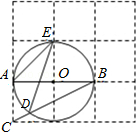
A.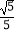
B.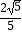
C.2
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,O是AC上一动点(不与点A、C重合),过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)OE与OF相等吗?证明你的结论;
(2)试确定点O的位置,使四边形AECF是矩形,并加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧
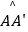 、
、 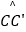 是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )
是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )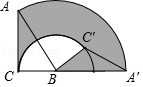
A.4π+2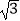
B.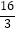
π﹣2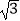
C.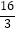
π+2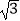
D.4π -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为﹣1,3,则下列结论正确的个数有( ) ①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意x均有ax2+bx≥a+b.
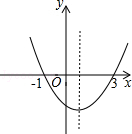
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,∠ADC的平分线交AB于点E,∠ABC的平分线交CD于点F,求证:四边形EBFD是平行四边形.

相关试题

