【题目】如图,E是△ABC中BC边上的一点,且BE= ![]() BC;点D是AC上一点,且AD=
BC;点D是AC上一点,且AD= ![]() AC,S△ABC=24,则S△BEF﹣S△ADF=( )
AC,S△ABC=24,则S△BEF﹣S△ADF=( ) 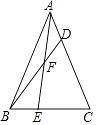
A.1
B.2
C.3
D.4
参考答案:
【答案】B
【解析】解:过D作DG∥AE交CE于G, ∵AD= ![]() AC,
AC,
∴CG=3EG,
∴AE= ![]() DG,CE=
DG,CE= ![]() CG,
CG,
∵EC=2BE,
∴BE=2EG,
∴EF= ![]() DG,
DG,
∴AF= ![]() DG,
DG,
∴EF=AF,
∵S△ABC=24,
∴S△ABD= ![]() S△ABC=6.
S△ABC=6.
∵EC=2BE,S△ABC=24,
∴S△ABE= ![]() S△ABC=8,
S△ABC=8,
∵S△ABE﹣S△ABD=(S△ABF+S△BEF)﹣(S△ADF+S△ABF)=S△BEF﹣S△ADF ,
即S△BEF﹣S△ADF=S△ABE﹣S△ABD=8﹣6=2.
故选B.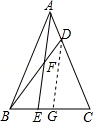
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为﹣1,3,则下列结论正确的个数有( ) ①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意x均有ax2+bx≥a+b.
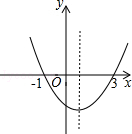
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,∠ADC的平分线交AB于点E,∠ABC的平分线交CD于点F,求证:四边形EBFD是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图∠1=∠2,CF⊥AB,DE⊥AB,求证:FG∥BC.
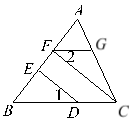
证明:∵CF⊥AB,DE⊥AB (已知)
∴∠BED=90°,∠BFC=90°( )
∴∠BED=∠BFC ( )
∴ED∥FC ( )
∴∠1=∠BCF ( )
∵∠2=∠1 ( 已知 )
∴∠2=∠BCF ( )
∴FG∥BC ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】小刚在课外书中看到这样一道有理数的混合运算题:
计算:

她发现,这个算式反映的是前后两部分的和,而这两部分之间存在着某种关系,利用这种关系,他顺利地解答了这道题。
(1)前后两部分之间存在着什么关系?
(2)先计算哪步分比较简便?并请计算比较简便的那部分。
(3)利用(1)中的关系,直接写出另一部分的结果。
(4)根据以上分析,求出原式的结果。
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)9+(﹣7)+10+(﹣3)+(﹣9)
(2)12+(﹣14)+6+(﹣7)
(3)﹣
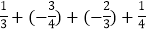
(4)﹣4.2+5.7+(﹣8.7)+4.2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm,求AE的长.

相关试题

