【题目】(问题情境)在综合实践课上,同学们以“图形的平移”为主题开展数学活动,如图①,先将一张长为4,宽为3的矩形纸片沿对角线剪开,拼成如图所示的四边形![]() ,
,![]() ,
,![]() ,则拼得的四边形
,则拼得的四边形![]() 的周长是_____.
的周长是_____.

(操作发现)将图①中的![]() 沿着射线
沿着射线![]() 方向平移,连结
方向平移,连结![]() 、
、![]() 、
、![]() 、
、![]() ,如图②.当
,如图②.当![]() 的平移距离是
的平移距离是![]() 的长度时,求四边形
的长度时,求四边形![]() 的周长.
的周长.
(操作探究)将图②中的![]() 继续沿着射线
继续沿着射线![]() 方向平移,其它条件不变,当四边形
方向平移,其它条件不变,当四边形![]() 是菱形时,将四边形
是菱形时,将四边形![]() 沿对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.
沿对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.
参考答案:
【答案】【问题情境】16;【操作发现】6+2![]() ;【操作探究】20或22.
;【操作探究】20或22.
【解析】
【问题情境】
首先由题意,可得AB=CD,AC=BD,∠ADB=∠DBC=90°,然后根据勾股定理,可得AB,即可求得四边形ABCD的周长;
【操作发现】
首先由平移,得AE=CF=3,DE=BF,再根据平行,即可判定四边形AECF是平行四边形,然后根据勾股定理,可得AF,即可求得四边形AECF的周长;
【操作探究】
首先由平移,得当点E与点F重合时,四边形ABCD为菱形,得出其对角线的长,沿对角线剪开的三角形组成的矩形有两种情况:以6为长,4为宽的矩形和以3为宽,8为长的矩形,即可求得其周长.
由题意,可得AB=CD,AC=BD,∠ADB=∠DBC=90°
又∵![]() ,
,![]() ,
,
∴根据勾股定理,可得![]()
∴四边形![]() 的周长是
的周长是![]()
故答案为16.
由平移,得AE=CF=3,DE=BF.
∵AE∥CF,
∴四边形AECF是平行四边形.
∵BE=DF=4,
∴EF=DE=2.
在Rt△AEF中,∠AEF=90°,
由勾股定理,得AF=![]() =
=![]() .
.
∴四边形AECF的周长为2AE+2AF=6+2![]() .
.
由平移,得当点E与点F重合时,四边形ABCD为菱形,AE=CE=3,BE=DE=4,沿对角线剪开的三角形组成的矩形有两种情况:
①以6为长,4为宽的矩形,其周长为![]() ;
;
②以3为宽,8为长的矩形,其周长为![]() .
.
故答案为20或22.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ACE中,CA=CE,∠CAE=30°,⊙O经过点C,且圆的直径AB在线段AE上.
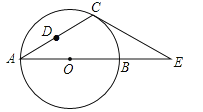
(1)试说明CE是⊙O的切线;
(2)若△ACE中AE边上的高为h,试用含h的代数式表示⊙O的直径AB;
(3)设点D是线段AC上任意一点(不含端点),连接OD,当
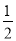 CD+OD的最小值为6时,求⊙O的直径AB的长.
CD+OD的最小值为6时,求⊙O的直径AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】现代营养学家用身体质量指数来判断人体的健康状态,这个指数等于人体质量(千克)与人体身高(米)平方得商,一个健康的人身体质量指数在20~25之间,身体质量指数低于18,属于不健康的瘦;身体质量指数高于30,属于不健康的胖。
(1)若一个人的质量为w千克,身高h米,用含字母w,h的代数式表示他的身体质量指数
(2)王先生的身高是1.75米,质量68千克,请判断他的身体是否健康。
-
科目: 来源: 题型:
查看答案和解析>>【题目】五一期间,甲、乙两人分别骑自行车和摩托车从
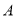 地出发前往
地出发前往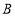 地郊游,并以各自的速度匀速行驶,到达目的地停止,途中乙休息了一段时间,然后又继续赶路.甲、乙两人各自行驶的路程
地郊游,并以各自的速度匀速行驶,到达目的地停止,途中乙休息了一段时间,然后又继续赶路.甲、乙两人各自行驶的路程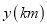 与所用时间
与所用时间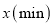 之间的函数图象如图所示.
之间的函数图象如图所示.
(1)甲骑自行车的速度是_____
 .
.(2)求乙休息后所行的路程
 与
与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围.
的取值范围.(3)为了保证及时联络,甲、乙两人在第一次相遇时约定此后两人之间的路程不超过
 .甲、乙两人是否符合约定,并说明理由.
.甲、乙两人是否符合约定,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2
 ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:设a+b
 (其中a、b、m、n均为整数),
(其中a、b、m、n均为整数),则有:a+b
 ,∴a=m2+2n2,b=2mn,这样小明就找到了一种把类似a+b
,∴a=m2+2n2,b=2mn,这样小明就找到了一种把类似a+b 的式子化为平方式的方法.
的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b
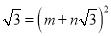 ,用含m、n的式子分别表示a、b得:a= ,b= ;
,用含m、n的式子分别表示a、b得:a= ,b= ;(2)利用所探索的结论,用完全平方式表示出:7+4
 = .
= .(3)请化简:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(-
 )+(+
)+(+ )-(-
)-(- )+(-
)+(- )
)(2)-54×
 ÷(-
÷(- )×
)×
(3)-29×
 -(-
-(- )+29×(-
)+29×(- )
)(4)(-
 -
- +
+ )÷(-
)÷(- )
)(5)-42+3×(-2)2+(-6)÷(-
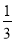 )2
)2(6)∣-
 ∣÷(
∣÷( -
- )-
)-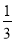 ×(-4)2
×(-4)2 -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
(1)a2+(5a2-2a)-2(a2-3a),其中a=-3.
(2)已知∣2a+1∣+(b-1)2=0,求:2(-
 a+
a+ b2)+(a-
b2)+(a- b2)-2(
b2)-2( a+b2)
a+b2)
相关试题

