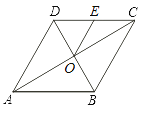
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是( )
A. ![]() B. 2 C.
B. 2 C. ![]() D. 4
D. 4
参考答案:
【答案】A
【解析】根据菱形的性质得菱形边长为4,AC⊥BD,由一个角是60度的等腰三角形是等边三角形得△ABD是等边三角形;在Rt△AOD中,根据勾股定理得AO=2![]() ,AC=2AO=4
,AC=2AO=4![]() ,根据三角形面积公式得S△ACD=
,根据三角形面积公式得S△ACD=![]() OD·AC=4
OD·AC=4![]() ,根据中位线定理得OE∥AD,根据相似三角形的面积比等于相似比继而可求出△OCE的面积.
,根据中位线定理得OE∥AD,根据相似三角形的面积比等于相似比继而可求出△OCE的面积.
∵菱形ABCD的周长为16,∴菱形ABCD的边长为4,
∵∠BAD=60°,
∴△ABD是等边三角形,
又∵O是菱形对角线AC、BD的交点,
∴AC⊥BD,
在Rt△AOD中,
∴AO=![]() ,
,
∴AC=2AO=4![]() ,
,
∴S△ACD=![]() OD·AC=
OD·AC= ![]() ×2×4
×2×4![]() =4
=4![]() ,
,
又∵O、E分别是中点,
∴OE∥AD,
∴△COE∽△CAD,
∴![]() ,
,
∴![]() ,
,
∴S△COE=![]() S△CAD=
S△CAD=![]() ×4
×4![]() =
=![]() ,
,
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】暑假期间,小明和父母一起开车到距家200千米的景点旅游.出发前,汽车油箱内储油45升;当行驶150千米时,发现油箱剩余油量为30升.
(1)已知油箱内余油量y(升)是行驶路程x(千米)的一次函数,求y与x的函数关系式;
(2)当油箱中余油量少于3升时,汽车将自动报警.如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知□ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1),解答下列问题:
(1)是否存在时刻t,使点P在∠BCD的平分线上;
(2)设四边形ANPM的面积为S(cm),求S与t之间的函数关系式;
(3)是否存在某一时刻t,使四边形ANPM与□ABCD面积相等,若存在,求出相应的t值,若不存在,说明理由;
(4)求t为何值时,△ABN为等腰三角形.
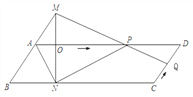
备用图
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折线ABC是在某市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.
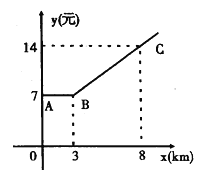
(1)根据图象,求当x≥3时的函数关系式;
(2)某人乘坐2.5km,应付多少钱?
(3)某人乘坐13km,应付多少钱?
(4)若某人付车费30.8元,出租车行驶了多少路程?
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
(x-1)(x+1)=x2-1;
(x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1
(x-1)(x4+x3+x2+x+1)=x5-1;
……
(1)猜想(x-1)(xn+xn-1+xn-2+…+x+1)=______.
运用上述规律,试求:
(2)219+218+217+…+23+22+2+1.
(3)52018+52017+52016+…+53+52+5+1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,反比例函数
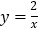 (x>0)与正比例函数y=kx、
(x>0)与正比例函数y=kx、 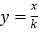 (k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
(k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.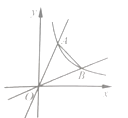
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
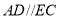 .
.(1)若
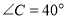 ,
,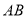 平分
平分 ,求
,求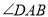 的度数;
的度数;(2)若
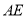 平分
平分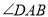 ,
, 平分
平分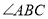 .
.①求证
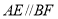 ;
;②将结论
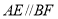 与条件
与条件 互换位置,其他条件不变,组成一个新的命题,判断该命题的真假,并写出证明过程.
互换位置,其他条件不变,组成一个新的命题,判断该命题的真假,并写出证明过程.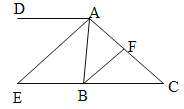
相关试题

