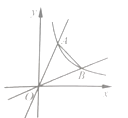
【题目】如图,在平面直角坐标系中,反比例函数![]() (x>0)与正比例函数y=kx、
(x>0)与正比例函数y=kx、 ![]() (k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
(k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
参考答案:
【答案】2
【解析】作BD⊥x轴,AC⊥y轴,OH⊥AB(如图),设A(x1,y1),B(x2 , y2),根据反比例函数k的几何意义得x1y1=x2y2=2;将反比例函数分别与y=kx,y=![]() 联立,解得x1=
联立,解得x1=![]() ,x2=
,x2=![]() ,从而得x1x2=2,所以y1=x2, y2=x1, 根据SAS得△ACO≌△BDO,由全等三角形性质得AO=BO,∠AOC=∠BOD,由垂直定义和已知条件得∠AOC=∠BOD=∠AOH=∠BOH=22.5°,根据AAS得△ACO≌△BDO≌△AHO≌△BHO,根据三角形面积公式得S△ABO=S△AHO+S△BHO=S△ACO+S△BDO=
,从而得x1x2=2,所以y1=x2, y2=x1, 根据SAS得△ACO≌△BDO,由全等三角形性质得AO=BO,∠AOC=∠BOD,由垂直定义和已知条件得∠AOC=∠BOD=∠AOH=∠BOH=22.5°,根据AAS得△ACO≌△BDO≌△AHO≌△BHO,根据三角形面积公式得S△ABO=S△AHO+S△BHO=S△ACO+S△BDO=![]() x1y1+
x1y1+ ![]() x2y2=
x2y2= ![]() ×2+
×2+ ![]() ×2=2.
×2=2.
如图:作BD⊥x轴,AC⊥y轴,OH⊥AB,
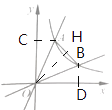
设A(x1,y1),B(x2 , y2),
∵A、B在反比例函数上,
∴x1y1=x2y2=2,
∵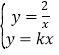 ,
,
解得:x1=![]() ,
,
又∵![]() ,
,
解得:x2=![]() ,
,
∴x1x2=![]() ×
×![]() =2,
=2,
∴y1=x2, y2=x1,
即OC=OD,AC=BD,
∵BD⊥x轴,AC⊥y轴,
∴∠ACO=∠BDO=90°,
∴△ACO≌△BDO(SAS),
∴AO=BO,∠AOC=∠BOD,
又∵∠AOB=45°,OH⊥AB,
∴∠AOC=∠BOD=∠AOH=∠BOH=22.5°,
∴△ACO≌△BDO≌△AHO≌△BHO,
∴S△ABO=S△AHO+S△BHO=S△ACO+S△BDO=![]() x1y1+
x1y1+ ![]() x2y2=
x2y2= ![]() ×2+
×2+ ![]() ×2=2,
×2=2,
故答案为:2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折线ABC是在某市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.
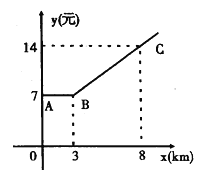
(1)根据图象,求当x≥3时的函数关系式;
(2)某人乘坐2.5km,应付多少钱?
(3)某人乘坐13km,应付多少钱?
(4)若某人付车费30.8元,出租车行驶了多少路程?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是( )
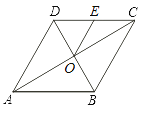
A.
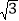 B. 2 C.
B. 2 C. 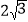 D. 4
D. 4 -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
(x-1)(x+1)=x2-1;
(x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1
(x-1)(x4+x3+x2+x+1)=x5-1;
……
(1)猜想(x-1)(xn+xn-1+xn-2+…+x+1)=______.
运用上述规律,试求:
(2)219+218+217+…+23+22+2+1.
(3)52018+52017+52016+…+53+52+5+1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
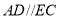 .
.(1)若
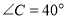 ,
,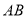 平分
平分 ,求
,求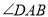 的度数;
的度数;(2)若
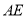 平分
平分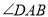 ,
, 平分
平分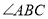 .
.①求证
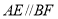 ;
;②将结论
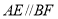 与条件
与条件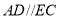 互换位置,其他条件不变,组成一个新的命题,判断该命题的真假,并写出证明过程.
互换位置,其他条件不变,组成一个新的命题,判断该命题的真假,并写出证明过程.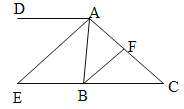
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,每个小正方形的边长均为
,每个小正方形的边长均为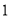 ,阴影部分是一个正方形.
,阴影部分是一个正方形.(1)阴影部分的面积是__________,边长是____________;
(2)写出不大于阴影正方形边长的所有正整数;
(3)
 为阴影正方形边长的小数部分,
为阴影正方形边长的小数部分, 为
为 的整数部分,求
的整数部分,求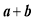 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将含有30°角的直角三角板ABC放入平面直角坐标系,顶点A,B分别落在x、y轴的正半轴上,∠OAB=60°,点A的坐标为(1,0),将三角板ABC沿x轴向右作无滑动的滚动(先绕点A按顺时针方向旋转60°,再绕点C按顺时针方向旋转90°,…)当点B第一次落在x轴上时,则点B运动的路径与坐标轴围成的图形面积是________.
相关试题

