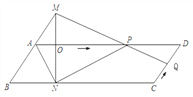
【题目】如图,已知□ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1),解答下列问题:
(1)是否存在时刻t,使点P在∠BCD的平分线上;
(2)设四边形ANPM的面积为S(cm),求S与t之间的函数关系式;
(3)是否存在某一时刻t,使四边形ANPM与□ABCD面积相等,若存在,求出相应的t值,若不存在,说明理由;
(4)求t为何值时,△ABN为等腰三角形.
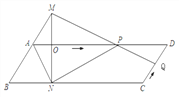
备用图
参考答案:
【答案】(1)![]() ;(2)
;(2) ![]() (0<t<1);(3)见解析;(4)
(0<t<1);(3)见解析;(4)![]() -1
-1
【解析】(1)当PC平分∠BCD时,则∠DCP=∠PCB, 由平行线的性质得到∠DPC=∠PCB,进而得到∠DPC=∠DCP, 由等角对等边得到DC=PD,代入求出即可;
(2)求出AP和MN的值,根据三角形的面积公式求出即可;
(3)假设存在某一时刻t,四边形ANPM的面积等于平行四边形ABCD的面积.根据(2)中求出的关系式,列方程求出t的值;
(4)分三种情况讨论:①AB=BN,②AB=AN,③BN=AN.
(1)当PC平分∠BCD时,则∠DCP=∠PCB, ∵AD∥BC, ∴∠DPC=∠PCB, ∴∠DPC=∠DCP, ∴DC=PD.
∵DC=1,PD=3-3t, ∴3-3t=1,3t=2,t=![]() .
.
(2)∵四边形ABCD是平行四边形,∴AB∥CD,∴∠MAP=∠QDP.
又∵∠MPA=∠QPD,∴△MAP∽△QDP.
∴![]() ∴
∴![]() ,解得:AM=t.
,解得:AM=t.
∵AB=CD=1,∴MB=1+t.
∵MN⊥BC,∠B=45°,∴sin45°=![]() ,∴MN=
,∴MN=![]() .
.
又∵四边形ABCD是平行四边形,∴AD∥BC又∵MN⊥BC,∴MN⊥AD,
∴SANPM=S△MAP+S△NAP=![]() APOM+
APOM+![]() APON=
APON=![]() AP(OM+ON)=
AP(OM+ON)=![]() APMN
APMN
=![]() =
=![]()
∴S与t之间的函数关系式为![]() (0<t<1);
(0<t<1);
(3)不存在.理由如下:
过A作AG⊥BC于G.
∵∠B=45°,AB=1,∴AG=![]() .
.
∵SANPM=SABCD,∴![]() =
=![]() ,∴
,∴![]() ,解得:t=-2,t=1.
,解得:t=-2,t=1.
∵0<t<1,∴不存在在某一时刻t,使四边形ANPM与□ABCD面积相等.
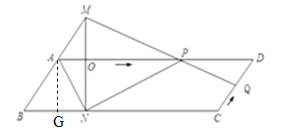
(4)由(2)可知:AM=t,∴BM=1+t.
∵∠B=45°,∴MN=BN=![]() .AD∥BC,∴∠MAD=∠B=45°,∠AOM=∠BNM=90°.
.AD∥BC,∴∠MAD=∠B=45°,∠AOM=∠BNM=90°.
∵AM=t, ∴AO=MO=![]() .
.
∵NO=AG=![]() ,∴AN=
,∴AN=![]() .分三种情况讨论:
.分三种情况讨论:
①当AB=BN时,![]() =1,解得:
=1,解得:![]() ;
;
②当AB=AN时,![]() =1,解得:t=1(舍去);
=1,解得:t=1(舍去);
③当BN=AN时,![]() =
=![]() 时,解得:t=0 (舍).
时,解得:t=0 (舍).
综上所述:当![]() 时,△ABN为等腰三角形.
时,△ABN为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB=α°,∠COD在∠AOB内部且∠COD=β°.
(1)若α,β满足|α-2β|+(β-60)2=0,则①α= ;
②试通过计算说明∠AOD与∠COB有何特殊关系;
(2)在(1)的条件下,如果作OE平分∠BOC,请求出∠AOC与∠DOE的数量关系;
(3)若α°,β°互补,作∠AOC,∠DOB的平分线OM,ON,试判断OM与ON的位置关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)平面上有四个点A,B,C,D,按照以下要求作图:
①作直线AD;
②作射线CB交直线AD于点E;
③连接AC,BD交于点F;
(2)图中共有 条线段;
(3)若图中F是AC的一个三等分点,AF<FC,已知线段AC上所有线段之和为18,求AF长.
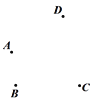
-
科目: 来源: 题型:
查看答案和解析>>【题目】暑假期间,小明和父母一起开车到距家200千米的景点旅游.出发前,汽车油箱内储油45升;当行驶150千米时,发现油箱剩余油量为30升.
(1)已知油箱内余油量y(升)是行驶路程x(千米)的一次函数,求y与x的函数关系式;
(2)当油箱中余油量少于3升时,汽车将自动报警.如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折线ABC是在某市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.
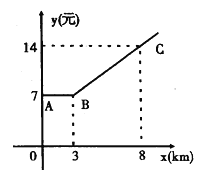
(1)根据图象,求当x≥3时的函数关系式;
(2)某人乘坐2.5km,应付多少钱?
(3)某人乘坐13km,应付多少钱?
(4)若某人付车费30.8元,出租车行驶了多少路程?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是( )
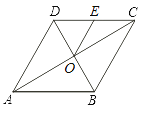
A.
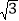 B. 2 C.
B. 2 C. 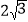 D. 4
D. 4 -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
(x-1)(x+1)=x2-1;
(x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1
(x-1)(x4+x3+x2+x+1)=x5-1;
……
(1)猜想(x-1)(xn+xn-1+xn-2+…+x+1)=______.
运用上述规律,试求:
(2)219+218+217+…+23+22+2+1.
(3)52018+52017+52016+…+53+52+5+1.
相关试题

