【题目】如图,AB是⊙O的直径,弦CD⊥AB于H.点G在⊙O上,过点G作直线EF,交CD延长线于点E,交AB的延长线于点F.连接AG交CD于K,且KE=GE.

(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若AC∥EF,![]() ,FB=1,求⊙O的半径.
,FB=1,求⊙O的半径.
参考答案:
【答案】(1)相切,理由见解析;(2)4.
【解析】
试题分析:(1)求出∠OGA=∠OAG,∠AKH+∠OAG=90°,∠KGE=∠GKE=∠AKH,推出∠KGE+∠OGA=∠AKH+∠OAG=90°,得出∠OGE=90°,根据切线的判定推出即可;
(2)求出∠F=∠CAH,∠OGF=∠CHA=90°,推出Rt△AHC∽Rt△FGO,得出![]() ,根据
,根据![]()
求出![]() ,得出方程
,得出方程![]() ,解出即可.
,解出即可.
试题解析:(1)如图,连接OG.
∵OA=OG,∴∠OGA=∠OAG.
∵CD⊥AB,∴∠AKH+∠OAG=90°.
∵KE=GE,
∴∠KGE=∠GKE=∠AKH.
∴∠KGE+∠OGA=∠AKH+∠OAG=90°.
∴∠OGE=90°,即OG⊥EF.
又∵G在圆O上,∴EF与圆O相切.
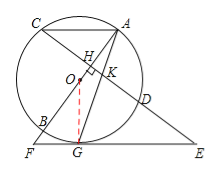
(2)∵AC∥EF, ∴∠F=∠CAH,
∴Rt△AHC∽ Rt△FGO. ∴![]() .
.
∵在Rt△OAH中,![]() ,设AH=3t,则AC=5t,CH=4t.
,设AH=3t,则AC=5t,CH=4t.
∴![]() . ∴
. ∴![]() .
.
∵FB=1 ∴![]() ,解得:OG=4.
,解得:OG=4.
∴圆O的半径为4 .
-
科目: 来源: 题型:
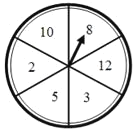
查看答案和解析>>【题目】小亮、小颖的手上都有两根长度分别为5、8的木棒,小亮与小颖都想通过转动转盘游戏来获取第三根木棒,如图,一个均匀的转盘被平均分成6等份,分别标有木棒的长度2,3,5,8,10,12这6个数字.小亮与小颖各转动转盘一次,停止后,指针指向的数字即为转出的第三根木棒的长度.若三根木棒能组成三角形则小亮获胜,三根木棒能组成等腰三角形则小颖获胜.
(1)小亮获胜的概率是 ;
(2)小颖获胜的概率是 ;
(3)请你用这个转盘设计一个游戏,使得对小亮与小颖均是公平的;
(4)小颖发现,她连续转动转盘10次,都没转到5和8,能不能就说小颖获胜的可能性为0?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=
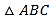 (x>0)的图象经过点C,交AB于点D.已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=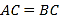 .
.(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.
-
科目: 来源: 题型:
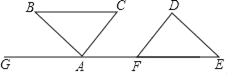
查看答案和解析>>【题目】如图,点A、F在线段GE上,AB∥DE,BC∥GE,AC∥DF,AB=DE
(1)请说明:△ABC≌△DEF;
(2)连接BF、CF、CE,请你判断BF与CE之间的关系?并说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,对角线AC与BD相交于点O,点E是BC上的一个动点,连接DE, 交 AC于点F.
(1)如图①,当
 时,求
时,求 的值;
的值;(2)如图②当DE平分∠CDB时,求证:AF=
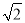 OA;
OA;(3)如图③,当点E是BC的中点时,过点F作FG⊥BC于点G,求证:CG=
 BG.
BG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y=ax2+bx+c(a≠0)的顶点为C(1,4),交x轴于A、B两点,交y轴于点 D,其中点B的坐标为(3,0).
(1)求抛物线的解析式;
(2)如图2,过点A的直线与抛物线交于点E,交y轴于点F,其中点E的横坐标为2,若直线PQ为抛物线的对称轴,点G为直线PQ上的一动点,则x轴上是否存在一点H,使D、G、H、F四点所围成的四边形周长最小;若存在,求出这个最小值及点G、H的坐标;若不存在,请说明理由.
(3)如图3,在抛物线上是否存在一点T,过点T作x轴的垂线,垂足为点M,过点M作MN∥BD,交线段AD于点N,连接MD,使△DNM∽△BMD。若存在,求出点T的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料并填空:
①(1﹣
 )(1+
)(1+ )=1﹣
)=1﹣ ,反过来,得1﹣
,反过来,得1﹣ =(1﹣
=(1﹣ )(1+
)(1+ )=
)= ×
× ;
;②(1﹣
 )(1+
)(1+ )=1﹣
)=1﹣ ,反过来,得1﹣
,反过来,得1﹣ =(1﹣
=(1﹣ )(1+
)(1+ )= × ;
)= × ;③(1﹣
 )(1+
)(1+ )=1﹣
)=1﹣ ,反过来,得1﹣
,反过来,得1﹣ = =
= = ;
;利用上面的材料中的方法和结论计算下题:
(1﹣
 )(1﹣
)(1﹣ )(1﹣
)(1﹣ )……(1﹣
)……(1﹣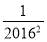 )(1﹣
)(1﹣ )(1﹣
)(1﹣ ).
).
相关试题

