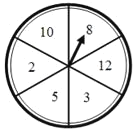
【题目】小亮、小颖的手上都有两根长度分别为5、8的木棒,小亮与小颖都想通过转动转盘游戏来获取第三根木棒,如图,一个均匀的转盘被平均分成6等份,分别标有木棒的长度2,3,5,8,10,12这6个数字.小亮与小颖各转动转盘一次,停止后,指针指向的数字即为转出的第三根木棒的长度.若三根木棒能组成三角形则小亮获胜,三根木棒能组成等腰三角形则小颖获胜.
(1)小亮获胜的概率是 ;
(2)小颖获胜的概率是 ;
(3)请你用这个转盘设计一个游戏,使得对小亮与小颖均是公平的;
(4)小颖发现,她连续转动转盘10次,都没转到5和8,能不能就说小颖获胜的可能性为0?为什么?
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析;(4)不能,理由见解析.
;(3)见解析;(4)不能,理由见解析.
【解析】
(1)设构成三角形的第三根木棒的长度为x,由三角形三边关系可知3<x<13,在所给的6个数字中,有4个数字满足条件,则可求小亮获胜的概率.(2)在所给的6个数字中,有2个数字满足条件,则可求小颖获胜的概率.(3)答案不唯一,只要使得小亮与小颖获胜的概率相同即可.(4)不能,只能说明可能性小,但并不一定为0.
解:
(1)设构成三角形的第三根木棒的长度为x,
则8﹣5<x<5+8,即3<x<13,
∵在2,3,5,8,10,12这6个数字中,能构成三角形的有5、8、10、12这四个,
∴小亮获胜的概率是![]() =
=![]() ,
,
故答案为:![]() .
.
(2)∵在2,3,5,8,10,12这6个数字中,能构成等腰三角形的有5,8这两个,
∴小颖获胜的概率是![]() =
=![]() .
.
(3)小亮转动转盘一次,停止后指针指向的数字即为转出的第三根木棒的长度.若三根木棒能组成三角形则小亮获胜;小颖转动转盘一次,停止后指针指向的数字为偶数,则小颖获胜.
(4)不能,她连续转动转盘10次,都没转到5和8,只是说明可能性小,但并不一定为0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.
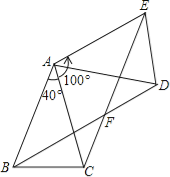
(1)求证:△ABD≌△ACE;
(2)求∠ACE的度数;
(3)求证:四边形ABFE是菱形.
-
科目: 来源: 题型:
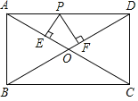
查看答案和解析>>【题目】已知:如图,矩形ABCD中,AB=5,BC=12,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥AC于点E,PF⊥BD于点F,则PE+PF等于( )
A.
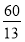 B.
B.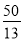 C.
C.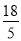 D.
D.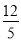
-
科目: 来源: 题型:
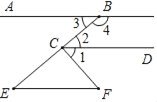
查看答案和解析>>【题目】把下面的推理过程补充完整,并在括号内填上理由.
已知:B、C、E三点在一条直线上,∠3=∠E,∠4+∠2=180°.
试说明:∠BCF=∠E+∠F
解:∵∠3=∠E(已知)
∴EF∥ (内错角相等,两直线平行)
∵∠4+∠2=180°(已知)
∴CD∥
∴CD∥ (平行于同一条直线的两条直线互相平行)
∴∠1=∠F,
∠2=
∵∠BCF=∠1+∠2(已知)
∴∠BCF=∠E+∠F(等量代换)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=
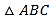 (x>0)的图象经过点C,交AB于点D.已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=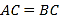 .
.(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.
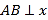
-
科目: 来源: 题型:
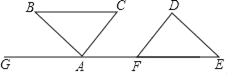
查看答案和解析>>【题目】如图,点A、F在线段GE上,AB∥DE,BC∥GE,AC∥DF,AB=DE
(1)请说明:△ABC≌△DEF;
(2)连接BF、CF、CE,请你判断BF与CE之间的关系?并说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB于H.点G在⊙O上,过点G作直线EF,交CD延长线于点E,交AB的延长线于点F.连接AG交CD于K,且KE=GE.

(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若AC∥EF,
 ,FB=1,求⊙O的半径.
,FB=1,求⊙O的半径.
相关试题

