搜索
【题目】如图，AB∥CD，CE平分∠ACD交AB于点E．
（1）求证：△ACE是等腰三角形．
（2）若AC=13，CE=10，求△ACE的面积．
参考答案：
【答案】（1）见解析；（2）60cm2
【解析】试题分析：（1）如图，证明∠AEC=∠ACE，即可解决问题．
（2）如图，作辅助线；求出AG的长度，运用三角形的面积公式，即可解决问题．
试题解析：（1）证明： ∵ CE平分ACD，∴ACE ECD．
∵ AB // CD，∴AEC ECD，∴ACE AEC，∴△ACE是等腰三角形；
（2）过A作AG⊥CE，垂足为G．
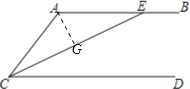
∵AC=AE，∴CG=EG=
CE=12（cm）．
∵AC=13（cm），由勾股定理得，AG=5（cm），∴S△ACE=
×24×5=60（cm2）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC中点，两边PE，PF分别交AB，AC于点E，F，给出以下五个结论：①△PFA≌△PEB，②EF=AP，③△PEF是等腰直角三角形，④当∠EPF在△ABC内绕顶点P旋转时（点E不与A，B重合），S四边形AEPF=
S△ABC，上述结论中始终正确有 （ ）
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】探究：如图①，在△ABC中，AB=AC，∠ABC=60°，延长BA至点D，延长CB至点E，使BE=AD，连结CD，AE，求证：△ACE≌△CBD．
应用：如图②，在菱形ABCF中，∠ABC=60°，延长BA至点D，延长CB至点E，使BE=AD，连结CD，EA，延长EA交CD于点G，求∠CGE的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】多项式x（x﹣1）﹣3x+4因式分解的结果等于 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】上周“双十二”瑞安某书店开展优惠购书活动：各类课外书活动时每本销售价格为y元，活动前每本销售价格为x（
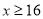）元，且y是x的一次函数，其中A类课外书与B类课外书活动前与活动时的价格如下表：图书类别
活动前的每本销售价格x（单位：元）
活动时的每本销售价格y
（单位：元）
A类
28
21
B类
21
18
（1）求y关于x的一次函数表达式.
（2）当天小明购买了一本课外书，花费了24元，该课外书活动前的每本销售价格是多少元？
（3）在“双十二”优惠活动中，某学校花费不超过1900元，购买A、B两类课外书共100本，且B类课外书不超过70本，则可能有哪几种购书方案？
-
科目： 来源： 题型：
查看答案和解析>>【题目】6张如图1的长为a，宽为b（a＞b）的小长方形纸片，按图2方式不重叠地放在矩形ABCD内，未被覆盖的部分（两个矩形）用阴影表示．设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（ ）
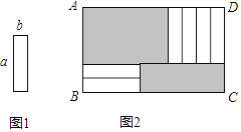
A. a=2b B. a=3b C. a=4b D. a=b
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两辆汽车沿同一路线从A地前往B地，甲以
千米/时的速度匀速行驶，途中出现故障后停车维修，修好后以
千米/时的速度继续行驶；乙在甲出发2小时后匀速前往B地，比甲早30分钟到达．到达B地后，乙按原速度返回A地，甲以
千米/时的速度返回A地．设甲、乙两车与A地相距s（千米），甲车离开A地的时间为t（时），s与t之间的函数图象如图所示．（1）求
的值．（2）求甲车维修所用时间．
（3）求两车在途中第二次相遇时t的值．
（4）请直接写出当两车相距40千米时，t的值或取值范围.
相关试题
