【题目】甲、乙两辆汽车沿同一路线从A地前往B地,甲以![]() 千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以
千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以![]() 千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,比甲早30分钟到达.到达B地后,乙按原速度返回A地,甲以
千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,比甲早30分钟到达.到达B地后,乙按原速度返回A地,甲以![]() 千米/时的速度返回A地.设甲、乙两车与A地相距s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.
千米/时的速度返回A地.设甲、乙两车与A地相距s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.
(1)求![]() 的值.
的值.
(2)求甲车维修所用时间.
(3)求两车在途中第二次相遇时t的值.
(4)请直接写出当两车相距40千米时,t的值或取值范围.

参考答案:
【答案】(1)a=40;(2)1小时;(3)t=![]() ;(4)
;(4) ![]()
【解析】试题分析:(1)由图象的数量关系,由速度=路程÷时间就可以直接求出结论;
(2)先由图象求出条件求出行驶后面路程的时间久可以求出维修用的时间;
(3)由图象求出BC和EF的解析式,然后由其解析式构成二元一次方程组就可以求出t的值;
(4)设乙车出发x小时时与甲车相距40km,通过函数图象有120-40=80x,或80x-120=40,可以求出t值,根据后面甲、乙速度相等而在维修好后甲乙之间刚好相距40,根据函数图象可以求出t的取值范围.
试题解析:
(1)由函数图象,得
a=120÷3=40
(2)由题意,得
5.5﹣3﹣120÷(40×2),
=2.5﹣1.5,
=1.
∴甲车维修的时间为1小时;
(3)∵甲车维修的时间是1小时,
∴B(4,120).
∵乙在甲出发2小时后匀速前往B地,比甲早30分钟到达.
∴E(5,240).
∴乙行驶的速度为:240÷3=80,
∴乙返回的时间为:240÷80=3,
∴F(8,0).
设BC的解析式为y1=k1t+b1,EF的解析式为y2=k2t+b2,由图象,得
![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,
∴y1=80t﹣200,y2=﹣80t+640,
当y1=y2时,
80t﹣200=﹣80t+640,
t=5.25.
∴两车在途中第二次相遇时t的值为5.25小时,
(4)当t=1时,两车相距40km,
设乙车出发x小时时与甲车相距40km,由题意及函数图象,得
120﹣40=80x,或80x﹣120=40
x=1,或x=2,
∴t=3,t=4.
∴由图象得:4<t≤5或5.5≤t≤8时,
综上所述,当t=1或t=3或4≤t≤5或5.5≤t≤8时两车相距40千米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,CE平分∠ACD交AB于点E.
(1)求证:△ACE是等腰三角形.
(2)若AC=13,CE=10,求△ACE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】上周“双十二”瑞安某书店开展优惠购书活动:各类课外书活动时每本销售价格为y元,活动前每本销售价格为x(
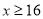 )元,且y是x的一次函数,其中A类课外书与B类课外书活动前与活动时的价格如下表:
)元,且y是x的一次函数,其中A类课外书与B类课外书活动前与活动时的价格如下表:图书类别
活动前的每本销售价格x(单位:元)
活动时的每本销售价格y
(单位:元)
A类
28
21
B类
21
18
(1)求y关于x的一次函数表达式.
(2)当天小明购买了一本课外书,花费了24元,该课外书活动前的每本销售价格是多少元?
(3)在“双十二”优惠活动中,某学校花费不超过1900元,购买A、B两类课外书共100本,且B类课外书不超过70本,则可能有哪几种购书方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】6张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
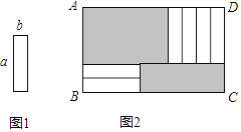
A. a=2b B. a=3b C. a=4b D. a=b
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数中( )
A.有最大的负数B.有最小的整数
C.有绝对值最小的数D.不是正有理数就是负有理数
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一次函数y=2x+b的图象不经过第二象限,则此函数的解析式可以为(写出一个即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中是假命题的是()
A.垂线段最短
B.两条直线被第三条直线所截,同位角相等
C.在同一平面内,垂直于同一直线的两条直线平行
D.不等式两边加同一个数,不等号的方向不变
相关试题

