【题目】小青在本学期的数学成绩如下表所示(成绩均取整数):

(1)计算小青本学期的平时平均成绩;
(2)如果学期的总评成绩是根据图所示的权重计算,那么本学期小青的期末考试成绩x至少为多少分才能保证达到总评成绩90分的最低目标?
参考答案:
【答案】(1)85(2)94分
【解析】解:(1)小青该学期的平时平均成绩为:(88+70+96+86)÷4=85. -------3分
(2)按照如图所示的权重,小青该学期的总评成绩为:85×10%+85×30%+60% x
--------5分
依题意得:85×10%+85×30%+60% x=90. --------6分
解得:x=93.33--------7分
答:小青期末考试成绩至少需要94分--------8分
(列不等式相应给分)
(1)平时成绩利用平均数公式. ![]() 计算;
计算;
(2)根据加权平均数公式列出方程,求得x的值即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店试销一种新商品,该商品的进价为40元/件,经过一段时间的试销发现,每月的销售量会因售价在40~70元之间的调整而不同.当售价在40~50元时,每月销售量都为60件;当售价在50~70元时,每月销售量与售价的关系如图所示,令每月销售量为y件,售价为x元/件,每月的总利润为Q元.
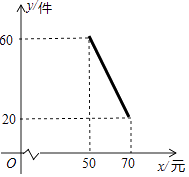
(1)当售价在50~70元时,求每月销售量为y与x的函数关系式?
(2)当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
(3)若该商店每月采购这种新商品的进货款不低于1760元,则该商品每月最大利润为元. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E为矩形ABCD中AD边中点,将矩形ABCD沿CE折叠,使点D落在矩形内部的点F处,延长CF交AB于点G,连接AF

(1)求证:AF∥CE;
(2)探究线段AF,EF,EC之间的数量关系,并说明理由;
(3)若BC=6,BG=8,求AF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°
(1) 求证:四边形ABCD是矩形
(2) 若DE⊥AC交BC于E,∠ADB∶∠CDB=2∶3,则∠BDE的度数是多少?
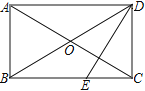
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB:y=kx+2k交x轴于点A,交y轴正半轴于点B,且S△OAB=3
(1) 求A、B两点的坐标
(2) 将直线AB绕A点顺时针旋转45°,交y轴于点C,求直线AC的解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某华为手机专卖店销售5台甲型手机和8台乙型手机的利润为1600元,销售15台甲型手机和6台乙型手机的利润为3000元
(1) 求每台甲型手机和乙型手机的利润
(2) 专卖店计划购进两种型号的华为手机共120台,其中乙型手机的进货量不低于甲型手机的2倍.设购进甲型手机x台,这120台手机全部销售的销售总利润为y元
① 直接写出y关于x的函数关系式_______________,x的取值范围是_______________
② 该商店如何进货才能使销售总利润最大?说明原因
(3) 专卖店预算员按照(2)中的方案准备进货,同时专卖店对甲型手机销售价格下调a元,结果预算员发现无论按照哪种进货方案最后销售总利润不变.请你判断有这种可能性吗?如果有,求出a的值;如果没有,说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】点E、F分别是□ABCD的边BC、CD上的点,∠EAF=60°,AF=4
(1) 若AB=2,点E与点B、点F与点D分别重合,求平行四边形ABCD的面积
(2) 若AB=BC,∠B=∠EAF=60°,求证:△AEF为等边三角形
(3) 若BE=CE,CF=2DF,AB=3,直接写出AE的长度(无需解答过程)
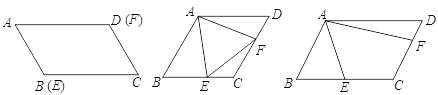
相关试题

