【题目】某华为手机专卖店销售5台甲型手机和8台乙型手机的利润为1600元,销售15台甲型手机和6台乙型手机的利润为3000元
(1) 求每台甲型手机和乙型手机的利润
(2) 专卖店计划购进两种型号的华为手机共120台,其中乙型手机的进货量不低于甲型手机的2倍.设购进甲型手机x台,这120台手机全部销售的销售总利润为y元
① 直接写出y关于x的函数关系式_______________,x的取值范围是_______________
② 该商店如何进货才能使销售总利润最大?说明原因
(3) 专卖店预算员按照(2)中的方案准备进货,同时专卖店对甲型手机销售价格下调a元,结果预算员发现无论按照哪种进货方案最后销售总利润不变.请你判断有这种可能性吗?如果有,求出a的值;如果没有,说明理由
参考答案:
【答案】(1)每台甲手机的利润为160元,每台乙手机的利润为100元(2)该商店购进40台A手机,80台B手机才能使销售总利润最大(3)有这种可能性
【解析】
(1)设每台甲型手机利润为x元,每台乙型手机的销售利润为y元;根据题意列出方程组求解,
(2)①据题意得,y=60x+12000;②利用不等式求出x的范围,又因为y=60x+12000是增函数,即可得出答案;
(3)据题意得,y=60x+12000-ax,0<x≤40进行求解.
(1)设每台甲手机的利润为x元,每台乙手机的利润为y元,由题意得:
![]() ,解得:
,解得:![]() ,
,
∴每台甲手机的利润为160元,每台乙手机的利润为100元;
(2)①y=60x+12000,0<x≤40且x为正整数,
故答案为:y=60x+12000;0<x≤40且x为正整数;
②∵y=60x+12000,0<x≤40且x为正整数,
∴k=60>0,y随x的增大而增大,
∴当x=40时,y=60×40+12000=14400最大,
即该商店购进40台A手机,80台B手机才能使销售总利润最大;
(3)有这种可能性,理由如下:
由题意可知:y=60x+12000-ax,0<x≤40且x为正整数,
∴y=(60-a)x+12000,
当60-a=0,即a=60时利润y=12000元与进货方案无关.
-
科目: 来源: 题型:
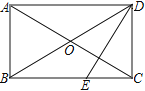
查看答案和解析>>【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°
(1) 求证:四边形ABCD是矩形
(2) 若DE⊥AC交BC于E,∠ADB∶∠CDB=2∶3,则∠BDE的度数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小青在本学期的数学成绩如下表所示(成绩均取整数):

(1)计算小青本学期的平时平均成绩;
(2)如果学期的总评成绩是根据图所示的权重计算,那么本学期小青的期末考试成绩x至少为多少分才能保证达到总评成绩90分的最低目标?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB:y=kx+2k交x轴于点A,交y轴正半轴于点B,且S△OAB=3
(1) 求A、B两点的坐标
(2) 将直线AB绕A点顺时针旋转45°,交y轴于点C,求直线AC的解析式.

-
科目: 来源: 题型:
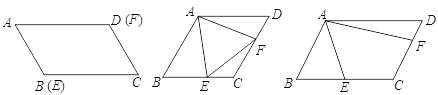
查看答案和解析>>【题目】点E、F分别是□ABCD的边BC、CD上的点,∠EAF=60°,AF=4
(1) 若AB=2,点E与点B、点F与点D分别重合,求平行四边形ABCD的面积
(2) 若AB=BC,∠B=∠EAF=60°,求证:△AEF为等边三角形
(3) 若BE=CE,CF=2DF,AB=3,直接写出AE的长度(无需解答过程)
-
科目: 来源: 题型:
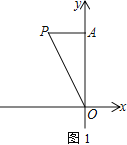
查看答案和解析>>【题目】如图,平面直角坐标系中,已知点A(0,5),点P(m,5)在第二象限,连接AP、OP
(1) 如图1,若OP=6,求m的值
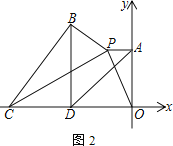
(2) 如图2,点C在x轴负半轴上,以CP为斜边作直角三角形BCP,∠CBP=90°,且∠BPC=∠APO.取OC的中点D,连接AD、BD,求证:AD=BD
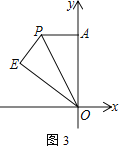
(3) 如图3,将△AOP沿直线OP翻折得到△EOP(点A的对应点为点E).若点E到x轴的距离不大于3,直接写出m的取值范围(无需解答过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把Rt△ACO以O点为中心,逆时针旋转90°,得Rt△BDO,点B坐标为(0,﹣3),点C坐标为(0,
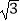 ),抛物线y=﹣
),抛物线y=﹣ 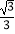 x2+bx+c经过点A和点C.
x2+bx+c经过点A和点C.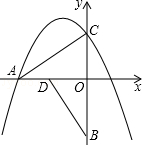
(1)求b,c的值;
(2)在x轴以上的抛物线对称轴上是否存在点Q,使得△ACQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由
(3)点P从点O出发沿x轴向负半轴运动,每秒1个单位,过点P作y轴的平行线交抛物线于点M,当t为几秒时,以M、P、O、C为顶点得四边形是平行四边形?
相关试题

