【题目】已知|x+2|+|1﹣x|=9﹣|y﹣5|﹣|1+y|,则x+y的最小值为_____,最大值为_____.
参考答案:
【答案】-3 6
【解析】
先将|x+2|+|1﹣x|=9﹣|y﹣5|﹣|1+y|化为|x+2|+|1﹣x|+|y﹣5|+|1+y|=9.分情况讨论可得当﹣2≤x≤1时,![]() 有最小值3,当﹣1≤y≤5时,
有最小值3,当﹣1≤y≤5时,![]() 有最小值6,从而根据|x+2|+|1﹣x|+|y﹣5|+|1+y|=9,可得x、y的取值范围,从而求得x+y的最小值和最大值.
有最小值6,从而根据|x+2|+|1﹣x|+|y﹣5|+|1+y|=9,可得x、y的取值范围,从而求得x+y的最小值和最大值.
解:因为|x+2|+|1﹣x|=9﹣|y﹣5|﹣|1+y|,
所以|x+2|+|1﹣x|+|y﹣5|+|1+y|=9,
当x≤-2时,![]() ,且当x=-2时,
,且当x=-2时,![]() 有最小值3,
有最小值3,
当﹣2<x<1时,![]() ,
,
当x≥1时,![]() ,且当x=1时,
,且当x=1时,![]() 有最小值3,
有最小值3,
故当﹣2≤x≤1时,![]() 有最小值3,
有最小值3,
当y≤﹣1时,![]() ,且当y=﹣1时,
,且当y=﹣1时,![]() 有最小值6,
有最小值6,
当﹣1<y<5时,![]() ,
,
当y≥5时,![]() ,且当y=5时,
,且当y=5时,![]() 有最小值6,
有最小值6,
故当﹣1≤y≤5时,![]() 有最小值6,
有最小值6,
所以,要使|x+2|+|1﹣x|+|y﹣5|+|1+y|=9,那么﹣2≤x≤1且﹣1≤y≤5,
故x+y最小值为﹣3,最大值为6.
故答案为:﹣3,6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条笔直的高速公路上依次有3个标志点A、B、C,甲、乙两车分别从A、C两点同时出发,匀速行驶,甲车从A→B→C,乙车从C→B→A,甲、乙两车离B的距离y1、y2(千米)与行驶时间x(小时)之间的函数关系图象如图所示.观察图象,给出下列结论:①A、C之间的路程为690千米;②乙车比甲车每小时快30千米;③4.5小时两车相遇;④点E的横坐标表示两车第二次相遇的时间;⑤点E的坐标为(7,180)其中正确的有________(把所有正确结论的序号都填在横线上).
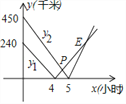
-
科目: 来源: 题型:
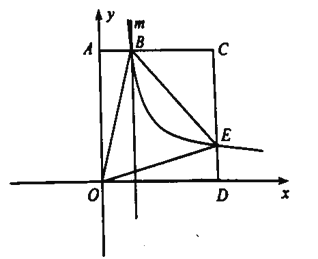
查看答案和解析>>【题目】如图,边长为3正方形
 的顶点
的顶点 与原点重合,点
与原点重合,点 在
在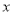 轴,
轴,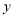 轴上。反比例函数
轴上。反比例函数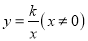 的图象交
的图象交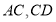 于点
于点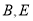 ,连接
,连接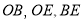 ,
,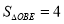 .
.(1)求反比例函数的解析式;
(2)过点
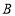 作
作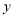 轴的平行线
轴的平行线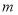 ,点
,点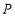 在直线
在直线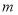 上运动,点
上运动,点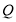 在
在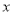 轴上运动.
轴上运动.①若
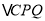 是以
是以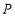 为直角顶点的等腰直角三角形,求
为直角顶点的等腰直角三角形,求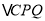 的面积;
的面积;②将“①”中的“以
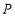 为直角顶点的”去掉,将问题改为“若
为直角顶点的”去掉,将问题改为“若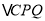 是等腰直角三角形”,
是等腰直角三角形”,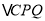 的面积除了“①”中求得的结果外,还可以是______.(直接写答案,不用写步骤)
的面积除了“①”中求得的结果外,还可以是______.(直接写答案,不用写步骤)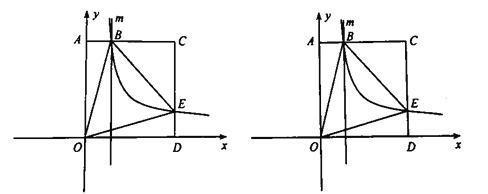
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两辆摩托车同时从相距20km的A,B两地出发,相向而行.图中l 1,l 2分别表示甲、乙两辆摩托车到A地的距离s(km)与行驶时间t(h)的函数关系.则下列说法错误的是( )

A.乙摩托车的速度较快B.经过0.3小时甲摩托车行驶到A,B两地的中点
C.当乙摩托车到达A地时,甲摩托车距离A地
 kmD.经过
kmD.经过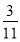 小时两摩托车相遇
小时两摩托车相遇 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系 xOy 中,正比例函数 y=kx 与一次函数 y=x+b 的图象相交于点 A(4,3).过点 P(2,0)作 x 轴的垂线,分别交正比例函数的图象于点 B,交一次函数的图象于点 C, 连接 OC.
(1)求这两个函数解析式;
(2)求△OBC 的面积;
(3)在 x 轴上是否存在点 M,使△AOM 为等腰三角形? 若存在,直接写出 M 点的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】现代营养学家用身体质量指数来判断人体的健康状态,这个指数等于人体质量(千克)与人体身高(米)平方得商,一个健康的人身体质量指数在20~25之间,身体质量指数低于18,属于不健康的瘦;身体质量指数高于30,属于不健康的胖。
(1)若一个人的质量为w千克,身高h米,用含字母w,h的代数式表示他的身体质量指数
(2)王先生的身高是1.75米,质量68千克,请判断他的身体是否健康。
-
科目: 来源: 题型:
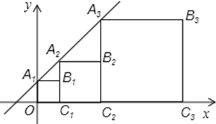
查看答案和解析>>【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则B5的坐标是_____________ 。
相关试题

