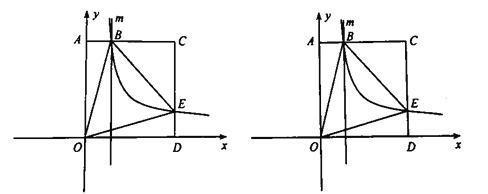
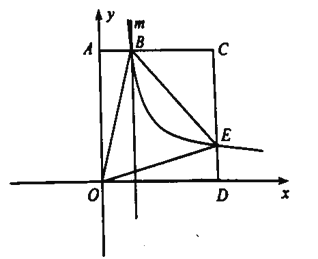
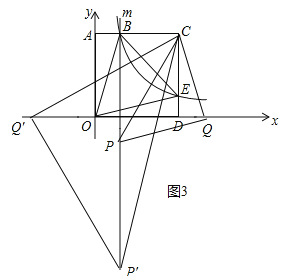
【题目】如图,边长为3正方形![]() 的顶点
的顶点![]() 与原点重合,点
与原点重合,点![]() 在
在![]() 轴,
轴,![]() 轴上。反比例函数
轴上。反比例函数![]() 的图象交
的图象交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求反比例函数的解析式;
(2)过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,点
,点![]() 在直线
在直线![]() 上运动,点
上运动,点![]() 在
在![]() 轴上运动.
轴上运动.
①若![]() 是以
是以![]() 为直角顶点的等腰直角三角形,求
为直角顶点的等腰直角三角形,求![]() 的面积;
的面积;
②将“①”中的“以![]() 为直角顶点的”去掉,将问题改为“若
为直角顶点的”去掉,将问题改为“若![]() 是等腰直角三角形”,
是等腰直角三角形”,![]() 的面积除了“①”中求得的结果外,还可以是______.(直接写答案,不用写步骤)
的面积除了“①”中求得的结果外,还可以是______.(直接写答案,不用写步骤)
参考答案:
【答案】(1)![]() ;(2)①
;(2)①![]() 或
或![]() .②5或17.
.②5或17.
【解析】
(1)设![]() 的坐标分别为
的坐标分别为![]() ,根据三角形的面积,构建方程即可解决问题.
,根据三角形的面积,构建方程即可解决问题.
(2)①分两种情形画出图形:当点P在线段BM上,当点P在线段BM的延长线上时,分别利用全等三角形的性质求解即可.
②当点Q是等腰三角形的直角顶点时,分两种情形分别求解即可.
解:(1))∵四边形OACD是正方形,边长为3,
∴点B的纵坐标为3,点E的横坐标为3,
∵反比例函数![]() 的图象交AC,CD于点B,E,
的图象交AC,CD于点B,E,
设![]() 的坐标分别为
的坐标分别为![]() .
.
∵S△OBE=4,
可得,![]() .
.
解得,![]() ,
,![]() (舍).
(舍).
所以,反比例函数的解析式为![]() .
.
(2))①如图1中,设直线m交OD于M.
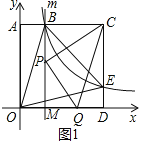
由(1)可知B(1,3),AB=1,BC=2,
当PC=PQ,∠CPQ=90°时,
∵∠CBP=∠PMQ=∠CPQ=90°,
∴∠CPB+∠BCP=90°,∠CPB+∠PQM=90°,
∴∠PCB=∠MPQ,∵PC=PQ,
∴△CBP≌△PMQ(AAS),
∴BC=PM=2,PB=MQ=1,
∴PC=PQ=![]()
∴S△PCQ=![]()
如图2中,当PQ=PC,∠CPQ=90°,
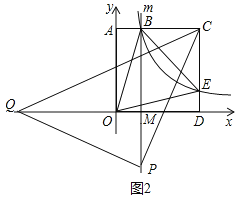
同法可得△CBP≌△PMQ(AAS),
∴PM=BC=2,OM=PB=5,
∴PC=PQ=![]() ,
,
∴S△PCQ=![]() .
.
所以,![]() 的面积为
的面积为![]() 或
或![]() .
.
②当点Q是等腰三角形的直角顶点时,同法可得CQ=PQ=![]() ,此时S△PCQ=5.
,此时S△PCQ=5.
或CQ′=PQ′=![]() ,可得S△P′CQ′=17,
,可得S△P′CQ′=17,
不存在点C为等腰三角形的直角顶点,
综上所述,△CPQ的面积除了“①”中求得的结果外,还可以是5或17.
故答案为5或17.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AC是弦,D是
 的中点,过点D作EF垂直于直线AC,垂足为F,交AB的延长线于点E.
的中点,过点D作EF垂直于直线AC,垂足为F,交AB的延长线于点E.(1)求证:EF是⊙O的切线;
(2)若tanA=
 ,AF=6,求⊙O的半径.
,AF=6,求⊙O的半径.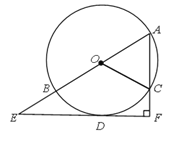
-
科目: 来源: 题型:
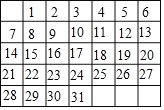
查看答案和解析>>【题目】如图是某月的月历,用一个矩形框,每次框住9个数.若这9个数之和是81,则这9个数中最大的数为_____,这9个数之和可能会是100吗?_____(填“能”或“不能”)
-
科目: 来源: 题型:
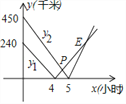
查看答案和解析>>【题目】在一条笔直的高速公路上依次有3个标志点A、B、C,甲、乙两车分别从A、C两点同时出发,匀速行驶,甲车从A→B→C,乙车从C→B→A,甲、乙两车离B的距离y1、y2(千米)与行驶时间x(小时)之间的函数关系图象如图所示.观察图象,给出下列结论:①A、C之间的路程为690千米;②乙车比甲车每小时快30千米;③4.5小时两车相遇;④点E的横坐标表示两车第二次相遇的时间;⑤点E的坐标为(7,180)其中正确的有________(把所有正确结论的序号都填在横线上).
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两辆摩托车同时从相距20km的A,B两地出发,相向而行.图中l 1,l 2分别表示甲、乙两辆摩托车到A地的距离s(km)与行驶时间t(h)的函数关系.则下列说法错误的是( )

A.乙摩托车的速度较快B.经过0.3小时甲摩托车行驶到A,B两地的中点
C.当乙摩托车到达A地时,甲摩托车距离A地
 kmD.经过
kmD.经过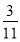 小时两摩托车相遇
小时两摩托车相遇 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知|x+2|+|1﹣x|=9﹣|y﹣5|﹣|1+y|,则x+y的最小值为_____,最大值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系 xOy 中,正比例函数 y=kx 与一次函数 y=x+b 的图象相交于点 A(4,3).过点 P(2,0)作 x 轴的垂线,分别交正比例函数的图象于点 B,交一次函数的图象于点 C, 连接 OC.
(1)求这两个函数解析式;
(2)求△OBC 的面积;
(3)在 x 轴上是否存在点 M,使△AOM 为等腰三角形? 若存在,直接写出 M 点的坐标;若不存在,请说明理由.

相关试题

