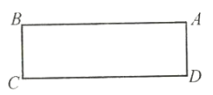
【题目】如图,在长方形![]() 中,
中,![]() ,
,![]() ,将长方形
,将长方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,点
,点![]() 、
、![]() 、
、![]() 分别对应点
分别对应点![]() 、
、![]() 、
、![]() .
.
(1)画出长方形![]() ;
;
(2)联结![]() 、
、![]() 、
、![]() ,请用含有
,请用含有![]() 、
、![]() 的代数式表示
的代数式表示![]() 的面积;
的面积;
(3)如果![]() 交
交![]() 于点
于点![]() ,请用含有
,请用含有![]() 、
、![]() 的代数式表示
的代数式表示![]() 的长度.
的长度.
参考答案:
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由题意知,A点旋转后对应点E正好落在边CD上,且DE=AD;线段DC的对应线段为DG,且![]() ,所以A、D、G三点共线,确定了D、E、G三点后,过点E作CD的垂线,过点G作DG的垂线,两条垂线的交点即为B的对应点F;
,所以A、D、G三点共线,确定了D、E、G三点后,过点E作CD的垂线,过点G作DG的垂线,两条垂线的交点即为B的对应点F;
(2)由旋转的性质可得FG、DG的长度,![]() ,AB//FG,从而所求三角形的面积为
,AB//FG,从而所求三角形的面积为![]() ;
;
(3)利用![]() ,结合(2)中所求
,结合(2)中所求![]() 的面积可求出线段DH,再求CH即可.
的面积可求出线段DH,再求CH即可.
(1)长方形![]() 如图:
如图:
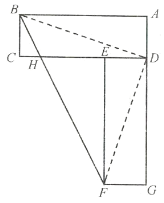
(2)由旋转图形的性质可知:
![]() ,
,![]() ,
,![]() ,
,
∴![]() ,即
,即![]() 、
、![]() 、
、![]() 三点共线,
三点共线,
∴![]()
![]()
![]() ;
;
(3)因为![]()
![]()
![]()
![]()
∴![]() ,
,
∴![]() ,
,
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正方形
 ,
, 为平面内任意一点,连接
为平面内任意一点,连接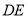 ,将线段
,将线段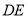 绕点
绕点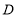 顺时针旋转
顺时针旋转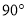 得到
得到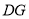 ,当点
,当点 ,
,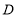 ,
,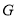 在一条直线时,若
在一条直线时,若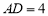 ,
,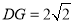 ,则
,则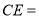 ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形
 中,长
中,长 ,宽
,宽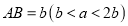 ,四边形
,四边形 和四边形
和四边形 都是正方形.
都是正方形.(1)求四边形
 的面积(用含
的面积(用含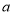 、
、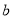 的代数式表示);
的代数式表示);(2)当
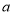 、
、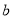 满足什么等量关系时,图形是一个轴对称图形.
满足什么等量关系时,图形是一个轴对称图形.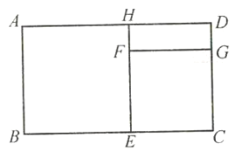
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:
①4a+c<0;②m(am+b)+b>a(m≠﹣1);③关于x的一元二次方程ax2+(b﹣1)x+c=0没有实数根;④ak4+bk2<a(k2+1)2+b(k2+1)(k为常数).其中正确结论的个数是( )
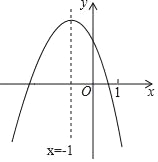
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简、在求值:
(1)(4a2-3a)-(1-4a+4a2),其中a=-2
(2)有8个算式,排成4行2列
2+2,2×2
3+
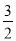 ,3×
,3×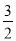
4+
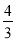 ,4×
,4×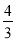
5+
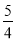 ,5×
,5×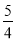
①同一行中两个算式的结果怎样?
②算式2019+
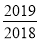 和2019×
和2019×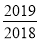 的结果相等吗?
的结果相等吗?③请你写出算式,试一试,再探索其规律,用含自然数n的代数式表示这一规律.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC、BD是菱形ABCD的对角线,那么下列结论一定正确的是( )
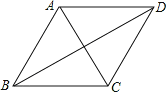
A. △ABD与△ABC的周长相等
B. △ABD与△ABC的面积相等
C. 菱形的周长等于两条对角线之和的两倍
D. 菱形的面积等于两条对角线之积的两倍
-
科目: 来源: 题型:
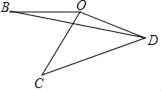
查看答案和解析>>【题目】将线段OB绕点O逆时针旋转60°得到线段OC,继续旋转α(0°<α<120°)得到线段OD,连接CD.
(1)如图,连接BD,则∠BDC的大小=_____(度);
(2)将线段OB放在平面直角坐标系中,O是坐标原点,点B的坐标为(﹣6,0),以OB为斜边作Rt△OBE,使∠OBE=∠OCD,且点E在第三象限,若∠CED=90°,则α的大小=_____(度),点D的坐标为_____.
相关试题

